题目内容
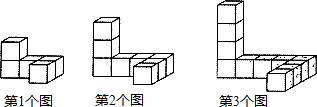
如图是由一些小正方体按一定规律组成的立体图形.
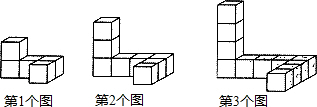
(1)用含n的式子表示第n个图中小正方形的个数;
(2)当n=3时,分别从正面,左面、上面观察这个图形,把能得到的平面图形画在下面相应的网格图中;
(3)若小正方体的棱长为1cm,请计算第3个图中立体图形的表面积.
 解:(1)n=1时,共有5个小正方形,n每增加1时,小正方形的个数都要增加3个,
解:(1)n=1时,共有5个小正方形,n每增加1时,小正方形的个数都要增加3个,所以第n个图形中小正方形的个数=3n+2;
(2)如图所示:
从正面看是1×5的矩形,最左侧的一块小正方形上面有1×3的矩形,
从左面看是1×4的矩形,最左侧的一块小正方形上面有1×3的矩形,
从上面看是1×5的矩形,最右侧的一块小正方形下面有1×3的矩形;
(3)∵小正方形的棱长为1cm,
∴小正方形的每个面的面积为1平方厘米,
∴(1×8+1×8+1×7)×2=46(平方厘米).
分析:(1)根据图形中小正方形的个数的变化得出答案即可;
(2)根据图3画出三视图即可;
(3)根据图形求出各侧面面积进而得出答案.
点评:此题主要考查了画三视图以及立体图形表面积求法和图形的变化类,注意三视图从不同角度观察得出答案.

练习册系列答案
相关题目
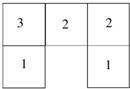 22、如图是由一些小正方体搭的几何体从上面看到的平面图形,小正方形内的数字表示在该位置上小正方体的个数,请画出它从正面和左面看到的平面图形.
22、如图是由一些小正方体搭的几何体从上面看到的平面图形,小正方形内的数字表示在该位置上小正方体的个数,请画出它从正面和左面看到的平面图形.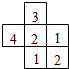 24、如图是由一些小正方体搭成的几何体从上面看到的平面图形,小正方形中的数字表示该位置上小正方体的个数,你能画出从它正面和左面看到的平面图形吗?试一试,你准行!
24、如图是由一些小正方体搭成的几何体从上面看到的平面图形,小正方形中的数字表示该位置上小正方体的个数,你能画出从它正面和左面看到的平面图形吗?试一试,你准行!