题目内容
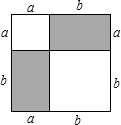数形结合思想是中学数学解题中常用的数学思想，利用这种思想，可以将代数问题转化为几何问题，也可以将几何问题转化为代数问题．通过数形结合将代数与几何完美的结合在一起，可以大大降低解题的难度，提高效率和正确率，甚至还可以达到令人意想不到的效果．教科书中利用几何图形证明乘法公式（a+b）2=a2+2ab+b2的做法，就是一个非常典型的例子：
如图，a、b分别表示一条线段的长度，则a+b可以表示两条线段之和，那么（a+b）2就可以表示正方形的面积．同样，a2、ab、b2也可以表示相应部分的面积，那么利用这种方法，就可以证明公式的正确性．
（1）请请你根据上述材料推导乘法公式（a+b+c）2的展开结果．
（2）若．a1、a2、b1、b2、c1、c2、d1、d2均为正数，且a1+a2=b1+b2=c1+c2=d1+d2=k，求证：a2b1+b2c1+c2d1+d2a1≤k2，并写出等号成立的条件．
解：（1）如图
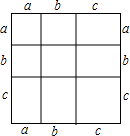
由图可得：（a+b+c）2=a2+b2+c2+2ab+2bc+2ca．
（2）由题意，可以构造边长为k的正方形，
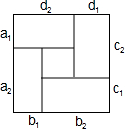
由图可得：a2b1，b2c1，c2d1，d2a1表示4个矩形的面积，它们之和小于正方形的面积，
∴a2b1+b2c1+c2d1+d2a1≤k2，当a1=a2=b1=b2=c1=c2=d1=d2时等号成立．
分析：（1）根据题意先画出图形，然后再根据图形得出（a+b+c）2的展开结果．
（2）先画出图形，由图形得出a2b1，b2c1，c2d1，d2a1表示4个矩形的面积，它们之和小于正方形的面积，从而得出a2b1+b2c1+c2d1+d2a1≤k2，即可证出a1=a2=b1=b2=c1=c2=d1=d2成立．
点评：本题考查对完全平方公式几何意义的理解，应从整体和部分两方面来理解完全平方公式的几何意义；主要围绕图形面积展开分析．
由图可得：（a+b+c）2=a2+b2+c2+2ab+2bc+2ca．
（2）由题意，可以构造边长为k的正方形，
由图可得：a2b1，b2c1，c2d1，d2a1表示4个矩形的面积，它们之和小于正方形的面积，
∴a2b1+b2c1+c2d1+d2a1≤k2，当a1=a2=b1=b2=c1=c2=d1=d2时等号成立．
分析：（1）根据题意先画出图形，然后再根据图形得出（a+b+c）2的展开结果．
（2）先画出图形，由图形得出a2b1，b2c1，c2d1，d2a1表示4个矩形的面积，它们之和小于正方形的面积，从而得出a2b1+b2c1+c2d1+d2a1≤k2，即可证出a1=a2=b1=b2=c1=c2=d1=d2成立．
点评：本题考查对完全平方公式几何意义的理解，应从整体和部分两方面来理解完全平方公式的几何意义；主要围绕图形面积展开分析．
练习册系列答案
相关题目