题目内容

已知等腰三角形的周长为24cm,腰长为x(cm),底边为y(cm),则底边y与x的函数关系式为         ，自变量x的取值范围是                    ．
（1）y=24-2x；（2）6＜x＜12．

试题分析：根据三角形周长公式可写出y与x的函数关系式；用三角形三边关系表示出x的取值范围．
试题解析：∵等腰三角形的周长为24cm，若底边长为ycm，一腰长为xcm．
∴2x+y=24，
∴y=24-2x；
∵①x-x＜y＜2x，
∴x-x＜24-2x＜2x，
∴x＞6，
∵②x-y＜x＜x+y，
∴x＜12，
∴自变量x的取值范围为：6＜x＜12．
练习册系列答案
相关题目
（2013年四川眉山3分）函数中，自变量x的取值范围是　 　．
水果店购进一箱橘子需要m元，已知橘子与箱子的总重量为a千克，箱子的重量为b千克．为了不亏本，这箱橘子的零售价至少应定为每千克______元．
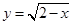在函数中，自变量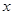的取值范围是         .；
函数中自变量x的取值范围是   ．
某商店为减少A商品的积压采取降价销售的策略．某商品原价为520元，随着不同幅度的降价，日销量（单位为件）发生相应的变化（如表）：
降价（元）
10
20
30
40
50
60
日销量（件）
155
160
165
170
175
180
 
（1）这个表反映了       和       两个变量之间的关系
（2）从表中可以看出每降价10元，日销量增加       件，
（3）可以估计降价之前的日销量为        件，
（4）如果售价为440元时，日销量为        件．
万州某运输公司的一艘轮船在长江上航行，往返于万州、朝天门两地．假设轮船在静水中的速度不变，长江的水流速度不变，该轮船从万州出发，逆水航行到朝天门，停留一段时间（卸货、装货、加燃料等），又顺水航行返回万州．若该轮船从万州出发后所用的时间为x（小时），轮船距万州的距离为y（千米），则下列各图形中，能够反映y与x之间函数关系的大致图象是（　　）
A．
B．
C．
D．
函数自变量x的取值范围是（　　）
A．x≥1且x≠3B．x≥1C．x≠3D．x＞1且x≠3
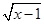函数y=＋3中自变量x的取值范围是（ ）
A．x＞1B．x≥1C．x≤1D．x≠1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网