题目内容
已知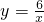
，利用反比例函数的增减性，求当x≤-2.5时，y的取值范围．
解：当x=-2.5时，y=-2.4，
∵比例系数为6，
∴y随x的减小而增大，
∵x≤-2.5，
∴函数图象在第三象限，y≥-2.4，
又y＜0．
∴-2.4≤y＜0．
故答案为：-2.4≤y＜0．
分析：先算出x=-2.5时，y的值，进而根据反比例函数的比例系数的符号可得图象所在象限及性质：y随x的减小而增大，那么可得y的取值范围．
点评：考查反比例函数的性质，求函数值的取值，应从所在象限及函数的增减性两方面考虑．
∵比例系数为6，
∴y随x的减小而增大，
∵x≤-2.5，
∴函数图象在第三象限，y≥-2.4，
又y＜0．
∴-2.4≤y＜0．
故答案为：-2.4≤y＜0．
分析：先算出x=-2.5时，y的值，进而根据反比例函数的比例系数的符号可得图象所在象限及性质：y随x的减小而增大，那么可得y的取值范围．
点评：考查反比例函数的性质，求函数值的取值，应从所在象限及函数的增减性两方面考虑．
练习册系列答案
相关题目
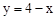与反比例函数
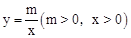的图象交于A、B两点，与x 轴、y轴分别相交于C、D两点。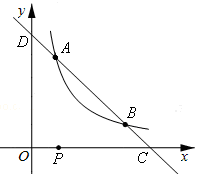
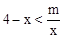的解集；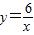
，利用反比例函数的增减性，求当x≤-2.5时，y的取值范围．