题目内容
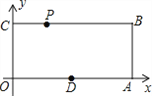
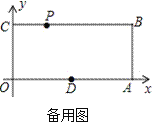
【题目】已知，如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在边BC上以每秒1个单位长的速度由点C向点B运动．
（1）当t为何值时，CP=OD？
（2）当△OPD为等腰三角形时，写出点P的坐标（请直接写出答案，不必写过程）．
（3）在线段PB上是否存在一点Q，使得四边形ODQP为菱形？若存在，求t的值，并求出Q点的坐标；若不存在，请说明理由.
【答案】（1）5；（2）（2，4），（2.5， 4），（3，4），（8， 4）；（3）（8，4）.
【解析】试题分析：
（1）由已知条件易得：OD=5，由CP=t=OD=5即可求得t的值；
（2）结合图形分：OP=DP、OP=OD和PD=OD三种情况分别讨论解答即可；
（3）由四边形ODQP是菱形可知：OP=OD=5，从而可求出点P此时的坐标，再由PQ=OD=5即可求得点Q的坐标.
试题解析：
（1）∵点A的坐标为（10，0），
∴OA=10，
∵点D是OA的中点,
∴OD=5，
又∵CP=t=OD=5，
∴t=5；
（2）点C的坐标为（0，4），CB∥
轴，点P在CB上运动，
∴点P的纵坐标为4.
△OPD为等腰三角形，存在以下三种情况：
I、当OP=DP时，点P在线段OD的垂直平分线上，
∴此时CP=t=
OD=2.5，
∴此时点P的坐标为（2.5，4）；
II、当OP=OD=5时，
在Rt△OPC中，由勾股定理可得：CP=
，
∴此时点P的坐标为（3，4）；
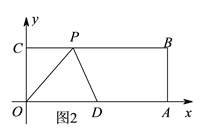
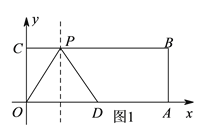
III、当PD=OD=5时，如图3，存在以下两种情况：
过点D作DE⊥BC于点E，则DE=OC=4，CE=OD=5，
在Rt△P1DE中，∵P1D=OD=5，
∴P1E=
，
∴CP1=CE-P1E=2，即此时点P1的坐标为（2，4）；
同理可得：点P2的坐标为（8，4）；
综上所述，当△OPD为等腰三角形时，点P的坐标为（2，4）、（2.5，4）、（3，4）和（8，4）；
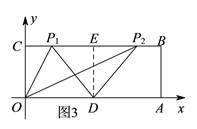
（3）如图4，∵四边形ODQP是菱形，
∴OP=OD=PQ=5，
由（2）可知，当OP=5时，CP=3，
∴CQ=CP+PQ=8，
又∵点P在线段CB上，
∴点Q的坐标为（8，4）.
