题目内容
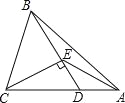
【题目】如图,△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.
求证:(1)DE=DA;(2)CE2=ADAC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据直角三角形30度角性质得到DE=![]() CD,根据已知条件AD=
CD,根据已知条件AD=![]() DC,由此不难证明.
DC,由此不难证明.
(2)先证明∠ECA=∠EAC=∠AED=30°,再证明△DEA∽△ECA即可.
试题解析:(1)∵CE⊥BD,∠BDC=60°
∴∠ECD=30°,
∴DE=![]() CD,又∵CD=2DA,即DA=
CD,又∵CD=2DA,即DA=![]() CD,
CD,
∴ED=DA.
(2)∵∠EDC=60°=∠DEA+∠DAE,
∵DE=DA,
∴∠DEA=∠DAE=30°,
∵∠ECD=30°,
∴∠ECA=∠EAC=∠AED=30°,
∴EC=EA,
∵∠EAD=∠CAE,∠AED=∠ACE
∴△DEA∽△ECA,
∴![]() ,
,
∴AE2=ADAC,∴EA=EC,
∴EC2=ADAC.

练习册系列答案
相关题目