题目内容
(1998•温州)抛物线y=x2-(2m-1)x-6m与x轴交于(x1,0)和(x2,0)两点,已知x1x2=x1+x2+49,要使此抛物线经过原点,应将它向右平移 个单位.
【答案】分析:确定抛物线与x轴的交点,再确定平移的单位长度.
解答:解:由根与系数关系得x1x2=-6m,x1+x2=2m-1,代入已知得-6m=2m-1+49,解得m=-6,
∴抛物线解析式为y=x2+13x+36=(x+4)(x+9),它与x轴两交点是(-4,0),(-9,0),故应将它向右平移4或9个单位,抛物线就可以经过原点.
点评:本题考查了根与系数关系,用待定系数法确定抛物线解析式.
解答:解:由根与系数关系得x1x2=-6m,x1+x2=2m-1,代入已知得-6m=2m-1+49,解得m=-6,
∴抛物线解析式为y=x2+13x+36=(x+4)(x+9),它与x轴两交点是(-4,0),(-9,0),故应将它向右平移4或9个单位,抛物线就可以经过原点.
点评:本题考查了根与系数关系,用待定系数法确定抛物线解析式.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
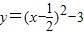 顶点坐标是 .
顶点坐标是 .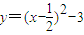 顶点坐标是 .
顶点坐标是 .