题目内容
【题目】如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性。
结论:(1) ;
(2) ;
(3) ;
(4) ;
选择结论: ,说明理由:
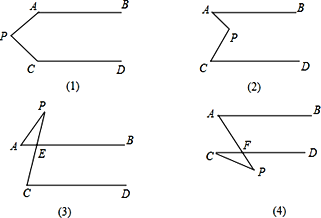
【答案】(1)∠APC+∠PAB+∠PCD=180°
(2)∠APC=∠PAB+∠PCD
(3)∠APC=∠PCD-∠PAB
(4)∠APC=∠PAB-∠PCD
【解析】试题分析:(1)过点P作PE∥AB,则AB∥PE∥CD,再根据两直线平行同旁内角互补即可解答;(2)过点P作PF∥AB,则AB∥CD∥l,再根据两直线内错角相等即可解答;(3)设AB与CP的交点为E,根据AB∥CD,可得出∠PEB=∠PCD,再根据三角形外角的性质进行解答;(4)设AB与CP的交点为E,根据AB∥CD,可得出∠PED=∠PAB,再根据三角形外角的性质进行解答.选择①即可.
试题解析:
(1)∠APC+∠PAB+∠PCD=180°
(2)∠APC=∠PAB+∠PCD
(3)∠APC=∠PCD-∠PAB
(4)∠APC=∠PAB-∠PCD
选择(1)
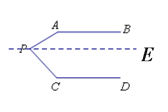
如图,过点P作PE∥CD则∠CPE+∠PCD=180°
∵CD∥AB
∴PE∥AB
∴∠APE+∠PAB=180°
∴∠APC+∠PAB+∠PCD=180°

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目