题目内容
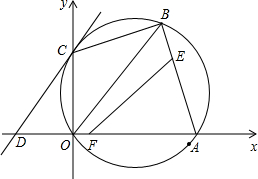 (2009•北仑区模拟)如图,在平面直角坐标系中,△OAB的外接圆交y轴于点C,已知点A的坐标(12,0),点B的坐标(
(2009•北仑区模拟)如图,在平面直角坐标系中,△OAB的外接圆交y轴于点C,已知点A的坐标(12,0),点B的坐标(| 600 |
| 169 |
| 1440 |
| 169 |
(1)求证:线段AB长度为12;
(2)求直线CD的解析式;
(3)设点E、F分别在边AB、AD上运动,且EF平分四边形ABCD的周长.试问,当线段AE等于多少时,△AEF的面积最大.
分析:(1)过点B作BM⊥OA于M,由点B、点A的坐标根据勾股定理就可以求出AB的长,从而求出结论.
(2)连接AC,作BN⊥OC于N,由圆周角的性质可以得出AC是直径,再由(1)的结论可以得出△AOC≌△ABC,而得出BC=OC,利用△ABM∽△CNB,可以求出BC,而求出C点的坐标,再根据切线的性质,由△AOC∽△COD,求出OD的值而求出D的坐标,最后由待定系数法就可以直接求出直线CD的解析式.
(3)作EH⊥OA于H,由勾股定理可以求出CD的值,可以求出四边形ABCD的周长,设AE=t,由条件可以表示出AF,由△AHE∽△AMB可以表示出EH,由三角形的面积公式表示出△AEF的面积,从而根据对称轴得出结论.
(2)连接AC,作BN⊥OC于N,由圆周角的性质可以得出AC是直径,再由(1)的结论可以得出△AOC≌△ABC,而得出BC=OC,利用△ABM∽△CNB,可以求出BC,而求出C点的坐标,再根据切线的性质,由△AOC∽△COD,求出OD的值而求出D的坐标,最后由待定系数法就可以直接求出直线CD的解析式.
(3)作EH⊥OA于H,由勾股定理可以求出CD的值,可以求出四边形ABCD的周长,设AE=t,由条件可以表示出AF,由△AHE∽△AMB可以表示出EH,由三角形的面积公式表示出△AEF的面积,从而根据对称轴得出结论.
解答: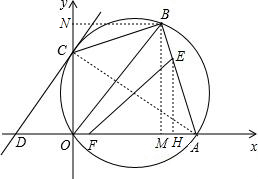 解:(1)证明:过点B作BM⊥OA于M,
解:(1)证明:过点B作BM⊥OA于M,
∴MB=
,OM=
.
∵OA=12,
∴AM=12-
=
,
∴AB=
=12;
(2)连接AC,作BN⊥OC于N,
∵∠AOC=90°,
∴AC是直径,
∴∠ABC=∠AOC=90°.
∵AB=AO=12,AC=AC,
∴△AOC≌△ABC,
∴BC=OC.
∵∠NBM=∠CBA=90°,
∴△AMB∽△CNB,
∴
=
,
∴
=
,
∴BC=5,
∴OC=5,
∴C(0,5).
∵CD切圆于点C,
∴∠DCA=90°=∠COD=∠COA,
∴∠CAO+∠ACO=∠ACO+∠DCO,
∴∠DCO=∠CAO,
∴△COD∽△CAO,
∴
=
,
∴
=
,
∴OD=
,
∴D(-
,0).
设直线CD的解析式为:y=kx+b,则
,
解得:
.
∴直线CD的解析式为:y=
x+5;
(3)设AE=t,CD=
=
,
∴四边形ABCD的周长为:12+5+
+
+12=36.5,
∴AF=18.25-t.
作EH⊥OA于H,
∴EH∥BM,
∴△AHE∽△AMB,
∴
=
,
∴
=
,
∴EH=
t,
∴S△AEF=
×
(18.25-t)=-
t2+
t,
∴当t=-
=-
=
时,△AEF的面积最大.
 解:(1)证明:过点B作BM⊥OA于M,
解:(1)证明:过点B作BM⊥OA于M,∴MB=
| 1440 |
| 169 |
| 600 |
| 169 |
∵OA=12,
∴AM=12-
| 600 |
| 169 |
| 1428 |
| 169 |
∴AB=
(
|
(2)连接AC,作BN⊥OC于N,
∵∠AOC=90°,
∴AC是直径,
∴∠ABC=∠AOC=90°.
∵AB=AO=12,AC=AC,
∴△AOC≌△ABC,
∴BC=OC.
∵∠NBM=∠CBA=90°,
∴△AMB∽△CNB,
∴
| BN |
| BM |
| BC |
| BA |
∴
| ||
|
| BC |
| 12 |
∴BC=5,
∴OC=5,
∴C(0,5).
∵CD切圆于点C,
∴∠DCA=90°=∠COD=∠COA,
∴∠CAO+∠ACO=∠ACO+∠DCO,
∴∠DCO=∠CAO,
∴△COD∽△CAO,
∴
| CO |
| AO |
| OD |
| OC |
∴
| 5 |
| 12 |
| OD |
| 5 |
∴OD=
| 25 |
| 12 |
∴D(-
| 25 |
| 12 |
设直线CD的解析式为:y=kx+b,则
|
解得:
|
∴直线CD的解析式为:y=
| 12 |
| 5 |
(3)设AE=t,CD=
52+ (
|
| 65 |
| 12 |
∴四边形ABCD的周长为:12+5+
| 65 |
| 12 |
| 25 |
| 12 |
∴AF=18.25-t.
作EH⊥OA于H,
∴EH∥BM,
∴△AHE∽△AMB,
∴
| EH |
| BM |
| AE |
| AB |
∴
| EH | ||
|
| t |
| 12 |
∴EH=
| 120 |
| 169 |
∴S△AEF=
| 1 |
| 2 |
| 120t |
| 169 |
| 60 |
| 169 |
| 1095 |
| 169 |
∴当t=-
| b |
| 2a |
| ||
2× -
|
| 73 |
| 8 |
点评:本题考查了切线的性质,待定系数法求一次函数的解析式,二次函数的最值,三角形的面积,相似三角形的判定与性质及勾股定理的运用.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
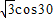 °;
°;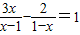 .
.