题目内容
【题目】如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1 , 点P的对应点为P1(a+6,b﹣2).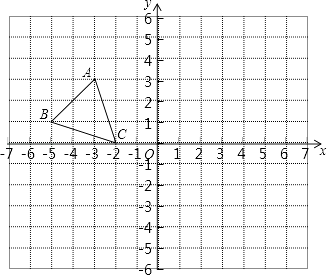
(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
【答案】
(1)
解:∵点P(a,b)的对应点为P1(a+6,b﹣2),
∴平移规律为向右6个单位,向下2个单位,
∴C(﹣2,0)的对应点C1的坐标为(4,﹣2)
(2)
解:△A1B1C1如图所示

(3)
解:△AOA1的面积=6×3﹣ ![]() ×3×3﹣
×3×3﹣ ![]() ×3×1﹣
×3×1﹣ ![]() ×6×2,
×6×2,
=18﹣ ![]() ﹣
﹣ ![]() ﹣6,
﹣6,
=18﹣12,
=6
【解析】(1)根据点P、P1的坐标确定出平移规律,再求出C1的坐标即可;(2)根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;(3)利用△AOA1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目