题目内容
如今手机的使用已经越来越普遍,不少大中学生也都有使用.现中国移动通信推出的业务当中有这样两种:“神州行”使用者不缴月租费,每通话1分钟(不足1分钟按1分钟计算)付话费0.6元,并赠送来电显示;“时尚通”使用者也不缴月租费,每通话1分钟(不足1分钟按1分钟计算)付话费0.4元,但不赠送来电显示,如有需要,每月需交10元的来电显示费用(这里均指市内通话的收费标准).若一个月内累计通话x(x为整数)分钟,“神州行”、“时尚通”两种通讯方式付话费分别为y1和y2元,
(1)用含x的代数式分别表示y1、y2;
(2)如果一个人计划月通话费不超过24元,那么他选择哪种通讯方式比较划算?
(3)一个月内通话多少分钟(都有来电显示),两种通讯方式的费用相同?
解:(1)由题意得
y1=0.6x,y2=0.4x+10;
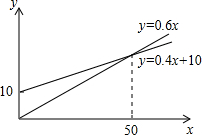
(2)在同一坐标系中画出这两个函数的图象
两个函数的图象交于点(50,30),
∵24<30,
∴他选神州行的通讯方式较省钱;
(3)两个函数的图象交于点(50,30),
这表示当x=50时,两个函数的值相都等于30,
因此,通话时间为50分钟,两种通讯方式的费用相同.
答:(1)y1=0.6x,y2=0.4x+10;(2)他选神州行的通讯方式较省钱;(3)通话时间为50分钟,两种通讯方式的费用相同.
分析:(1)根据:神州行的缴费=每分钟话费×时间,时尚通的缴费=每分钟话费×时间+来电显示费
写出神州行的缴费y1、时尚通的缴费y2与x之间的函数关系式;
(2)根据(1)画出两种方式的函数图象,并求出交点的坐标.
(3)根据(2)中计算与图象,可知.
点评:本题考查一次函数的应用.方程(组)、不等式与函数之间相互联系,用函数的观点可以把它们统一起来.解决问题时,应根据具体情况灵活地把它们结合起来考虑.
y1=0.6x,y2=0.4x+10;
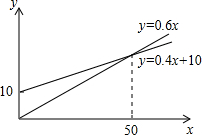
(2)在同一坐标系中画出这两个函数的图象
两个函数的图象交于点(50,30),
∵24<30,
∴他选神州行的通讯方式较省钱;
(3)两个函数的图象交于点(50,30),
这表示当x=50时,两个函数的值相都等于30,
因此,通话时间为50分钟,两种通讯方式的费用相同.
答:(1)y1=0.6x,y2=0.4x+10;(2)他选神州行的通讯方式较省钱;(3)通话时间为50分钟,两种通讯方式的费用相同.
分析:(1)根据:神州行的缴费=每分钟话费×时间,时尚通的缴费=每分钟话费×时间+来电显示费
写出神州行的缴费y1、时尚通的缴费y2与x之间的函数关系式;
(2)根据(1)画出两种方式的函数图象,并求出交点的坐标.
(3)根据(2)中计算与图象,可知.
点评:本题考查一次函数的应用.方程(组)、不等式与函数之间相互联系,用函数的观点可以把它们统一起来.解决问题时,应根据具体情况灵活地把它们结合起来考虑.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目