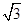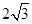题目内容
已知在三角形纸片ABC中,∠C=90度,BC=1,AC=2,如果将这张三角形纸片折叠,使点A与点B重合,折痕交AC于点M,那么AM=________.

分析:首先根据题意作出图形,根据折叠的性质即可知:MN是线段AB的垂直平分线,则可证得:AM=BM,在Rt△BCM中,由勾股定理,借助于方程求解即可.
解答:
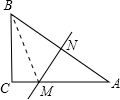 解:如图:连接BM,
解:如图:连接BM,∵将这张三角形纸片折叠,使点A与点B重合,折痕交AC于点M,
∴MN是线段AB的垂直平分线,
∴BM=AM,
设AM=x,则BM=x,CM=AC-AM=2-x,
∵∠C=90°,
∴BC2+CM2=BM2,
∴1+(2-x)2=x2,
解得:x=
 .
.∴AM=
 .
.故答案为:
 .
.点评:此题考查了折叠的性质与勾股定理的应用.解此题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
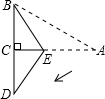 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°.在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )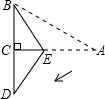 如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕翻折△ABC,使AB的一部分与BC重合,A与BC延长线上的点D重合,则线段AD的长度为( )
如图所示,已知在三角形纸片ABC中,BC=3,AB=6,∠BCA=90°,在AC上取一点E,以BE为折痕翻折△ABC,使AB的一部分与BC重合,A与BC延长线上的点D重合,则线段AD的长度为( ) 重合,则DE的长度为
重合,则DE的长度为 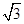


 重合,则DE的长度为
重合,则DE的长度为