题目内容
已知：二次函数y＝x2＋bx＋c与x轴相交于A(x1，0)、B(x2，0)两点，其顶点坐标为P(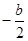
，
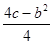)，AB＝|x1－x2|，若S△APB＝1，则b与c的关系式是（ ）．
| A．b2－4c＋1＝0 | B．b2－4c－1＝0 | C．b2－4c＋4＝0 | D．b2－4c－4＝0 |
D
解析试题分析：由于抛物线顶点坐标为P(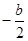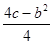，)，AB＝|x1－x2|，根据根与系数的关系把AB的长度用b、c表示，而S△APB＝1，然后根据三角形的面积公式就可以建立关于b、c的等式．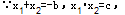
∴
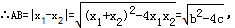
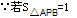
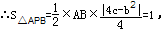
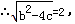
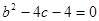
故选D.
考点：抛物线与x轴的交点情况与判别式的关系、抛物线顶点坐标公式、三角形的面积公式
点评：本题综合性强，难度较大，是中考常见题，题目比较典型.
练习册系列答案
阅读快车系列答案
相关题目
x2－x＋4．
x2＋bx＋c，其图象对称轴为直线x＝1，且经过点(2，－
)．
．
，
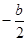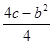)，AB＝|x1－x2|，若S△APB＝1，则b与c的关系式是（ ）．