题目内容
园林队在某公园进行绿化，中间休息了一段时间．已知绿化面积
（单位：平方米）与工作时间
（单位：小时）的函数关系的图象如图所示，则休息后园林队每小时绿化面积为
| A．40平方米 | B．50平方米 | C．80平方米 | D．100平方米 |
B
解析试题分析：由图象可知休息后共工作了4-2=2小时，完成160-60=100平方米，因此休息后园林队每小时绿化面积为100÷2=50平方米
考点：一次函数的图象
练习册系列答案
相关题目
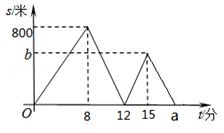
小明、小宇从学校出发到青少年宫参加书法比赛，小明步行一段时间后，小宇骑自行车沿相同路线行进，两人均匀速前行．他们的路程差s（米）与小明出发时间t（分）之间的函数关系如图所示．下列说法：①小宇先到达青少年宫；②小宇的速度是小明速度的3倍；③a=20；④b=600．其中正确的是（ ）
| A．①②③ | B．①②④ | C．①③④ | D．①②③④ |
已知点A在双曲线
上，点B在直线
上，且A，B两点关于轴对称，设点A的坐标为（
，
），则
+
的值是( )
| A．-10 | B．-8 | C．6 | D．4 |
等腰三角形的周长是40cm，腰长y (cm)是底边长x (cm)的函数解析式正确的是（ ）
| A．y=－0.5x+20 ( 0<x<20)&nbs, | B．y=－0.5x+20 (10<x<20) &nbs, |
| C．y=－2x+40 (10<x<20)&nbs, | D．y=－2x+40 (0<x<20)&nbs, |
在同一直角坐标系下，直线y=x+1与双曲线
的交点的个数为（ ）
| A．0个 | B．1个 | C．2个 | D．不能确定 |
已知正比例函数y=kx（k≠0）的图象经过点（1，-2），则这个正比例函数的解析式为（ ）
| A．y=2x&nbs, | B．y=?2x&nbs, | C．y= x&nbs, | D．y=?x&nbs, |