题目内容
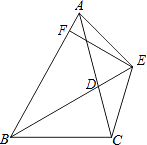
【题目】如图1,等边△ABC边长为6,AD是△ABC的中线,P为线段AD(不包括端点A、D)上一动点,以CP为一边且在CP左下方作如图所示的等边△CPE,连结BE.
(1)点P在运动过程中,线段BE与AP始终相等吗?说说你的理由;
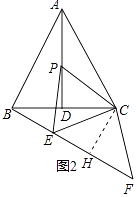
(2)若延长BE至F,使得CF=CE=5,如图2,问:求出此时AP的长;
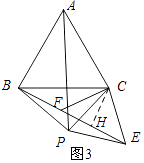
(3)当点P在线段AD的延长线上时,F为线段BE上一点,使得CF=CE=5.求EF的长
【答案】
(1)
解:BE=AP;理由如下:
∵△ABC和△CPE均为等边三角形,
∴∠ACB=∠PCE=60°,AC=BC,CP=CE.
∵∠ACP+∠DCP=∠DCE+∠PCD=60°,
∴∠ACP=∠BCE.
∵在△ACP和△BCE中, 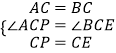 ,
,
∴△ACP≌△BCE(SAS).
∴BE=AP
(2)
解:如图2所示:过点C作CH⊥BE,垂足为H.∵AB=AC,AD是BC的中点,
∴∠CAD=∠BAD= ![]() ∠BAC=30°.
∠BAC=30°.
∵由(1)可知:△ACP≌△BCE,
∴∠CBE=∠CAD=30°,AP=BE.
∵在Rt△BCH中,∠HBC=30°,
∴HC= ![]() BC=3,BH=
BC=3,BH= ![]() BC=3
BC=3 ![]() .
.
∵在Rt△CEH中,EC=5,CH=3,
∴EH= ![]() =
= ![]() =4.
=4.
∴BE=HB﹣EH=3 ![]() ﹣4.
﹣4.
∴AP=3 ![]() ﹣4
﹣4
(3)
解:如图3所示:过点C作CH⊥BE,垂足为H.
∵△ABC和△CEP均为等边三角形,
∴AC=BC,CE=PC,∠ACB=∠ECP.
∴∠ACB+∠BCP=∠ECP+BCP,即∠BCE=∠ACP.
∵在△ACP和△BCE中, 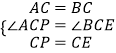 ,
,
∴△ACP≌△BCE(SAS).
∴∠CBH=∠CAP=30°.
∵在Rt△BCH中,∠CBH=30°,
∴HC= ![]() BC=3.
BC=3.
∵FC=CE,CH⊥FE,
∴FH=EH.
∴FH=EH= ![]() =
= ![]() =4.
=4.
∴EF=FH+EH=4+4=8.
【解析】(1)证出∠ACP=∠BCE.由SAS证明△ACP≌△BCE,得出对应边相等即可.(2)过点C作CH⊥BE,垂足为H.由等边三角形的性质得出∠CAD=∠BAD= ![]() ∠BAC=30°.由(1)可知:△ACP≌△BCE,得出∠CBE=∠CAD=30°,AP=BE.由含30°角的直角三角形的性质得出HC=
∠BAC=30°.由(1)可知:△ACP≌△BCE,得出∠CBE=∠CAD=30°,AP=BE.由含30°角的直角三角形的性质得出HC= ![]() BC=3,由勾股定理得出BH=
BC=3,由勾股定理得出BH= ![]() BC=3
BC=3 ![]() .在Rt△CEH中,由勾股定理求出EH=
.在Rt△CEH中,由勾股定理求出EH= ![]() =4,即可得出AP的长.(3)过点C作CH⊥BE,垂足为H.由SAS证明△ACP≌△BCE,得出∠CBH=∠CAP=30°.由含30°角的直角三角形的性质得出HC=
=4,即可得出AP的长.(3)过点C作CH⊥BE,垂足为H.由SAS证明△ACP≌△BCE,得出∠CBH=∠CAP=30°.由含30°角的直角三角形的性质得出HC= ![]() BC=3.与等腰三角形的性质求出FH=EH.由勾股定理求出FH,即可得出EF的长.
BC=3.与等腰三角形的性质求出FH=EH.由勾股定理求出FH,即可得出EF的长.
【考点精析】认真审题,首先需要了解全等三角形的性质(全等三角形的对应边相等; 全等三角形的对应角相等).

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于54000元的金额在采购这两种型号的净水器共30台,求A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这30台净水器能否实现利润为12800元的目标?若能,请给出相应的采购方案;若不能,请说明理由.