题目内容
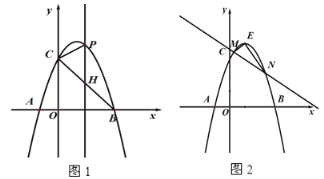
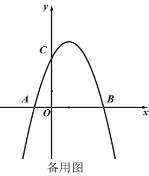
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
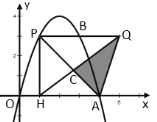
(2)点![]() 是第一象限抛物线上一动点,过点
是第一象限抛物线上一动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,交
,交![]() 于点
于点![]() .当△
.当△![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
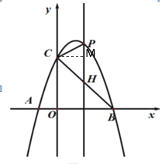
(3)如图2,抛物线顶点为![]() ,已知直线
,已知直线![]() 与二次函数图象相交于
与二次函数图象相交于![]() ,
,![]() 两点.求证:无论
两点.求证:无论![]() 为何值,△
为何值,△![]() 恒为直角三角形.
恒为直角三角形.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标
的坐标![]() ,
,![]() ,
,![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)将点![]() 代入解析式中即可求出结论;
代入解析式中即可求出结论;
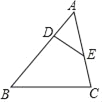
(2)利用待定系数法求出直线BC的解析式,设点![]() ,则点
,则点 ![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,根据等腰三角形腰的情况分类讨论,然后根据三线合一、等腰直角三角形的性质列出方程即可求出结论;
,根据等腰三角形腰的情况分类讨论,然后根据三线合一、等腰直角三角形的性质列出方程即可求出结论;
(3)将二次函数和一次函数的解析式联立,整理得![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,根据根与系数的关系可得则
,根据根与系数的关系可得则![]() ,
, ![]()
![]() ,
,![]() ,然后利用平面直角坐标系中任意两点之间的距离公式和勾股定理的逆定理即可证出结论.
,然后利用平面直角坐标系中任意两点之间的距离公式和勾股定理的逆定理即可证出结论.
解:(1)将点![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() ,
,
∴![]() ;
;
(2)设直线![]() 的解析式为
的解析式为![]() ,
,
将点![]() 代入
代入![]() ,
,
得,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
设点![]() ,则点
,则点 ![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,
,
![]()
①当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
解得,![]() (舍去),
(舍去),![]() ,
,
∴![]() ;
;
②当![]() 时,
时,
![]() ,
,
解得![]()
∴![]()
③当![]() 时,此时点P和点M重合
时,此时点P和点M重合
![]() ,
,
解得![]()
∴![]()
综上所述点![]() 的坐标
的坐标![]() ,
,![]() ,
,![]() ;
;
(3)将二次函数与直线![]() 的表达式联立并整理得:
的表达式联立并整理得:![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
则![]()
![]() ,
,
同理:![]() ,
,
点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
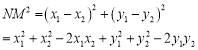
![]()
![]()
![]()
∴![]()
即:![]() 为直角三角形.
为直角三角形.

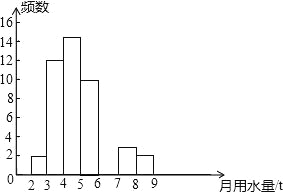
【题目】小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | a | b |
5≤x<6 | 10 | 20% |
6≤x<7 | c | 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)频数分布表中a= ,b= .(填百分比),c= ;补全频数分布直方图.
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有 户;
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率.