题目内容
如图①,平面直角坐标系中,已知C(0,10),点P、Q同时从点O出发,在线段OC上做往返匀速运动,设运动时间为t(s),点P、Q离开点O的距离为S,图②中线段OA、OB(A、B都在格点上)分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t(s)的函数图象.
(1)请在图②中分别画出当6≤t≤10时P、Q两点离开点O的距离S与运动时间t(s)的函数图象.
(2)求出P、Q两点第一次相遇的时刻.
(3)如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围).

(1)请在图②中分别画出当6≤t≤10时P、Q两点离开点O的距离S与运动时间t(s)的函数图象.
(2)求出P、Q两点第一次相遇的时刻.
(3)如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围).

考点:二次函数综合题
专题:压轴题,图表型,分类讨论
分析:(1)根据0≤t≤6时的函数图象求出P、Q的速度,再求出P到达10时的时间,然后补全图形,求出Q到达10时的时间,以及10秒时的路程,再补全图形即可;
(2)根据相遇时,点P、Q行驶的路程之和等于OC的2倍列出方程求解即可;
(3)分①点Q到达点C前,②点Q到达点C后返回至相遇前,重合部分为两个等腰直角三角形的面积的差,③P、Q相遇后,没有重合部分三种情况列式整理即可得解.
(2)根据相遇时,点P、Q行驶的路程之和等于OC的2倍列出方程求解即可;
(3)分①点Q到达点C前,②点Q到达点C后返回至相遇前,重合部分为两个等腰直角三角形的面积的差,③P、Q相遇后,没有重合部分三种情况列式整理即可得解.
解答: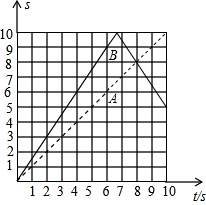 解:(1)由图可知,点P的速度为:6÷6=1单位/秒,
解:(1)由图可知,点P的速度为:6÷6=1单位/秒,
点Q的速度为:9÷6=
单位/秒,
∴点P到达点C的时间为10÷1=10秒,
点Q到达点C的时间为10÷
=
秒,
10秒时,返回的路程为10×1.5-10=5单位,
补全图形如图所示;
(2)设t秒时,P、Q两点第一次相遇,
由题意得,t+
t=10×2,
解得t=8;
(3)①点Q到达点C前,0≤t≤
,
重合部分面积y=
t2-
[t-(
t-t)]2,
=
t2-
t2,
=
t2;
②点Q到达点C后返回至相遇前,
<t<8,
重合部分面积y=
t2-
[t-(20-
t-t)]2,
=
t2-
(
t-20)2,
=-
t2+70t-200,
③P、Q相遇后,8≤t≤10,没有重合部分,
所以,y=0.
 解:(1)由图可知,点P的速度为:6÷6=1单位/秒,
解:(1)由图可知,点P的速度为:6÷6=1单位/秒,点Q的速度为:9÷6=
| 3 |
| 2 |
∴点P到达点C的时间为10÷1=10秒,
点Q到达点C的时间为10÷
| 3 |
| 2 |
| 20 |
| 3 |
10秒时,返回的路程为10×1.5-10=5单位,
补全图形如图所示;
(2)设t秒时,P、Q两点第一次相遇,
由题意得,t+
| 3 |
| 2 |
解得t=8;
(3)①点Q到达点C前,0≤t≤
| 20 |
| 3 |
重合部分面积y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 8 |
=
| 3 |
| 8 |
②点Q到达点C后返回至相遇前,
| 20 |
| 3 |
重合部分面积y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
=-
| 45 |
| 8 |
③P、Q相遇后,8≤t≤10,没有重合部分,
所以,y=0.
点评:本题是二次函数综合题型,主要利用了路程、速度、时间三者之间的关系,相遇问题的等量关系,难点在于(3)分情况讨论并判断出重合部分是两个等腰直角三角形的面积的差.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,△ABC和△DCE都是等边三角形,且B、C、E在一直线上.
如图,△ABC和△DCE都是等边三角形,且B、C、E在一直线上. 如图,是由几个小立方块搭成的几何体的俯视图,小正方形的数字表示该位置小立方块的个数,请画出相应的几何体的主视图及左视图.
如图,是由几个小立方块搭成的几何体的俯视图,小正方形的数字表示该位置小立方块的个数,请画出相应的几何体的主视图及左视图. 如图,P是正方形ABCD内一点,以正方形ABCD的一条边做为对角线,点P与这条边的两个端点作平行四边形,依次得点E、F、G、H,求证:四边形EFGH是正方形.
如图,P是正方形ABCD内一点,以正方形ABCD的一条边做为对角线,点P与这条边的两个端点作平行四边形,依次得点E、F、G、H,求证:四边形EFGH是正方形.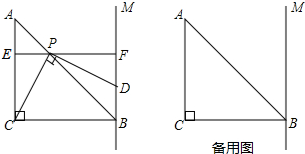
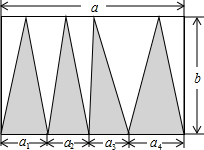 如图,长方形的长为a,宽为b,试说明长方形中带有阴影的三角形的面积之和等于该长方形面积的一半.
如图,长方形的长为a,宽为b,试说明长方形中带有阴影的三角形的面积之和等于该长方形面积的一半. 如图,在等腰Rt△ABC中,∠B=90°,AB=BC=8cm.动点P从点A出发沿线段AB向点B运动,动点Q从点C出发沿射线BC运动,连接PQ,交AC于点D.作PE⊥AC于点E,若在点P,Q运动的过程中,始终保持AP=CQ,则线段DE的长度为
如图,在等腰Rt△ABC中,∠B=90°,AB=BC=8cm.动点P从点A出发沿线段AB向点B运动,动点Q从点C出发沿射线BC运动,连接PQ,交AC于点D.作PE⊥AC于点E,若在点P,Q运动的过程中,始终保持AP=CQ,则线段DE的长度为