题目内容
从-2,-1,1,2,3这五个数中随机抽取一数,作为函数y=mx2+2mx+2中的m的值,若能使函数与x轴有两个不同的交点A、B,与y轴的交点为C,且△ABC的面积大于 的概率为:
的概率为:
 的概率为:
的概率为: 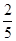 .
.试题分析:先确定五个中能使函数与x轴有两个不同的交点函数与x轴有两个不同的交点的个数,再计算面积大于
 的概率即可.
的概率即可.试题解析:要使二次函数的图象与x轴有两个交点,必须△=b2-4ac>0.
即:4m2-8m>0,
在-2,-1,1,2,3这五个数中能使△>0的有-2,-1,3;
令y=0,则mx2+2mx+2=0
当m=-2时,x2+2x-1=0,解得:
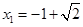 ,
,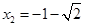 .
.∴AB=
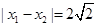 ,OC=2
,OC=2S△ABC=
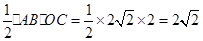 >
> ;
;同理:当m=-1时,S△ABC=
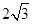 >
> ;
;当m=3时,S△ABC=
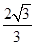 <
<
所以满足条件的概率为
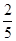 .
.考点: 1.概率公式;2.抛物线与x轴的交点.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
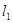 ∥
∥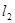 ,点A,B,C在直线
,点A,B,C在直线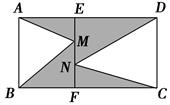
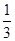 B.
B.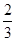 C.
C.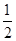 D.
D.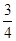




 ,则小烈手里共有扑克牌( )
,则小烈手里共有扑克牌( )