题目内容
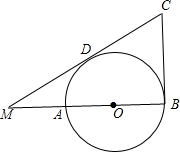 如图,△MBC中,∠B=90°,∠C=60°,MB=
如图,△MBC中,∠B=90°,∠C=60°,MB= ,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为
,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为
- A.

- B.

- C.2
- D.3
C
分析:在直角三角形BCM中,根据60°的正切函数以及MB的长度,求出BC的长,然后根据AB为直径且AB与BC垂直,得到BC为圆O的切线,又因为CD也为圆O的切线,根据切线长定理得到切线长CD与BC相等,即可得到CD的长.
解答:在直角△BCM中,
tan60°= =
= ,
,
得到BC=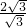 =2,
=2,
∵AB为圆O的直径,且AB⊥BC,
∴BC为圆O的切线,又CD也为圆O的切线,
∴CD=BC=2.
故选C
点评:此题考查学生灵活运用三角函数解直角三角形,掌握圆外一点引圆的两条切线,切线长相等的应用,是一道中档题.
分析:在直角三角形BCM中,根据60°的正切函数以及MB的长度,求出BC的长,然后根据AB为直径且AB与BC垂直,得到BC为圆O的切线,又因为CD也为圆O的切线,根据切线长定理得到切线长CD与BC相等,即可得到CD的长.
解答:在直角△BCM中,
tan60°=
 =
= ,
,得到BC=
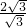 =2,
=2,∵AB为圆O的直径,且AB⊥BC,
∴BC为圆O的切线,又CD也为圆O的切线,
∴CD=BC=2.
故选C
点评:此题考查学生灵活运用三角函数解直角三角形,掌握圆外一点引圆的两条切线,切线长相等的应用,是一道中档题.

练习册系列答案
相关题目
 如图,△MBC中,∠B=90°,∠C=60°,MB=
如图,△MBC中,∠B=90°,∠C=60°,MB= ,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为
,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为  B.
B.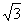 C.2 D.3
C.2 D.3
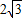 ,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为( )
,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为( )


 ,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为( )
,点A在MB上,以AB为直径作⊙O与MC相切于点D,则CD的长为( )


