Question

【题目】已知在平面直角坐标系中，抛物线与x轴相交于点A，B，与y轴相交于点C，直线y=x+4经过A，C两点，

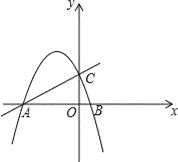
（1）求抛物线的表达式；

（2）如果点P，Q在抛物线上（P点在对称轴左边），且PQ∥AO，PQ=2AO，求P，Q的坐标；

（3）动点M在直线y=x+4上，且△ABC与△COM相似，求点M的坐标．

Answer 1

【答案】（1）（2）P点坐标（﹣5，﹣），Q点坐标（3，﹣）（3）M点的坐标为（﹣，），（﹣3，1）

【解析】

试题（1）根据自变量与函数值的对应关系，可得A、C点坐标，根据待定系数法，可得函数解析式；

（2）根据平行于x轴的直线与抛物线的交点关于对称轴对称，可得P、Q关于直线x=﹣1对称，根据PQ的长，可得P点的横坐标，Q点的横坐标，根据自变量与函数值的对应关系，可得答案；

（3）根据两组对边对应成比例且夹角相等的两个三角形相似，可得CM的长，根据等腰直角三角形的性质，可得MH的长，再根据自变量与函数值的对应关系，可得答案．

试题解析：（1）当x=0时，y=4，即C（0，4），

当y=0时，x+4=0，解得x=﹣4，即A（﹣4，0），

将A、C点坐标代入函数解析式，得

，

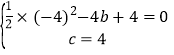解得，

抛物线的表达式为；

（2）PQ=2AO=8，

又PQ∥AO，即P、Q关于对称轴x=﹣1对称，

PQ=8，﹣1﹣4=﹣5，

当x=﹣5时，y=×（﹣5）2﹣（﹣5）+4=﹣，即P（﹣5，﹣）；

﹣1+4=3，即Q（3，﹣）；

P点坐标（﹣5，﹣），Q点坐标（3，﹣）；

（3）∠MCO=∠CAB=45°，

①当△MCO∽△CAB时，，即，

CM=．

如图1，

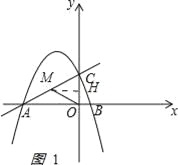
过M作MH⊥y轴于H，MH=CH=CM=，

当x=﹣时，y=﹣+4=，

∴M（﹣，）；

当△OCM∽△CAB时，，即，解得CM=3，

如图2，

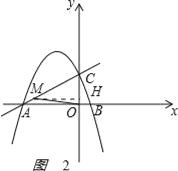
过M作MH⊥y轴于H，MH=CH=CM=3，

当x=﹣3时，y=﹣3+4=1，

∴M（﹣3，1），

综上所述：M点的坐标为（﹣，），（﹣3，1）．