题目内容
若正三角形、正方形、正六边形的周长相等,它们的面积分别为S1,S2,S3,则下列关系成立的是
- A.S1=S2=S3
- B.S1>S2>S3
- C.S1<S2<S3
- D.S2>S3>S1
C
分析:根据三角形、正方形、正六边形的周长相等可设出三角形的边长,再求出S1,S2,S3,的值进行比较即可.
解答:设正三角形的边长为a,则正方形的边长为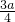 ,正六边形的边长为
,正六边形的边长为 ;
;
∵正三角形的边长为a,
∴其高为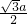 ,
,
∴S1= a×
a×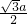 =
=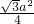 ;
;
S2=(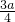 )2=
)2= ;
;
∵正六边形的边长为 ,
,
∴把正六边形分成六个三角形,其高为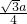 ,
,
∴S3=6× ×
× ×
×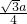 =
= .
.
∵S1=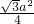 =
=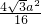 ,S3=
,S3= =
= ,
,
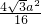 <
< <
< ,
,
∴S1<S2<S3.
故选C.
点评:此题考查的是正三角形、正方形、正六边形面积的求法,属中等难度题目.
分析:根据三角形、正方形、正六边形的周长相等可设出三角形的边长,再求出S1,S2,S3,的值进行比较即可.
解答:设正三角形的边长为a,则正方形的边长为
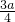 ,正六边形的边长为
,正六边形的边长为 ;
;∵正三角形的边长为a,
∴其高为
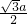 ,
,∴S1=
 a×
a×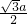 =
=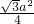 ;
;S2=(
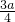 )2=
)2= ;
;∵正六边形的边长为
 ,
,∴把正六边形分成六个三角形,其高为
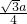 ,
,∴S3=6×
 ×
× ×
×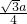 =
= .
.∵S1=
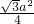 =
=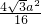 ,S3=
,S3= =
= ,
,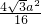 <
< <
< ,
,∴S1<S2<S3.
故选C.
点评:此题考查的是正三角形、正方形、正六边形面积的求法,属中等难度题目.

练习册系列答案
相关题目
若正三角形、正方形、正六边形的周长相等,它们的面积分别为S1,S2,S3,则下列关系成立的是( )
| A、S1=S2=S3 | B、S1>S2>S3 | C、S1<S2<S3 | D、S2>S3>S1 |