题目内容
【题目】在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(﹣4,0),将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
(1)请在图中画出△AEF.
(2)请在x轴上找一个点P,使PA+PE的值最小,并直接写出P点的坐标为 .
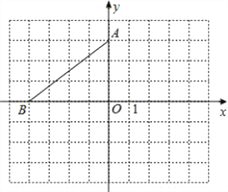
【答案】(1)作图见解析;(2)P点坐标为(1.5,0).
【解析】试题分析:(1)利用网格特点和旋转的性质画出点O和B的对应点E、F,从而得到△AEF;
(2)作点A关于x轴的对称点A′,连结EA′交x轴于P点,如图,则PA=PA′,于是可得到PA+PE=EA′,根据两点之间线段最短可判断此时PA+PB最小,然后利用OP=![]() AE=
AE=![]() 可写出P点坐标.
可写出P点坐标.
试题解析:(1)如图,△AEF为所作;
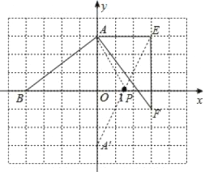
(2)作点A关于x轴的对称点A′,连结EA′交x轴于P点,如图,
因为PA=PA′,所以PA+PE=PA′+PE=EA′,所以此时PA+PB的值最小,
因为OP=0.5AE=1.5,所以P点坐标为(1.5,0).

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目