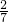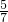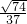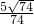题目内容
(1)计算:-2sin30°-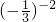 +
+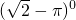 -
-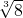 +(-1)2012
+(-1)2012
(2)解方程: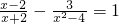 .
.
(1)解:原式=-2× -9+1-2+1,
-9+1-2+1,
=-1-9+1-2+1,
=-10;
(2)解:方程两边都乘以(x+2)(x-2)得:
(x-2)(x-2)-3=x2-4,
解这个方程得:x2-4x+4-3-x2+4=0,
-4x=-5,
x= ,
,
∵检验:把x= 代入(x+2)(x-2)≠0,
代入(x+2)(x-2)≠0,
∴x= 是原方程的解.
是原方程的解.
分析:(1)分别求出每一部分的值:sin30°= ,
,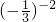 =9,
=9,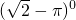 =1,
=1,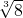 =2,(-1)2012=1,再代入求出即可;
=2,(-1)2012=1,再代入求出即可;
(2)方程的两边乘以(x+2)(x-2)得出方程(x-2)(x-2)-3=x2-4,求出方程的解,在代入(x+2)(x-2)进行检验即可.
点评:本题考查了负指数幂,零指数幂,特殊角的三角函数值,解分式方程等知识点的应用,解(1)的关键是求出每一部分的值,解(2)的关键是把分式方程转化成整式方程,题目都较好,但是(1)小题是一道比较容易出错的题目.
 -9+1-2+1,
-9+1-2+1,=-1-9+1-2+1,
=-10;
(2)解:方程两边都乘以(x+2)(x-2)得:
(x-2)(x-2)-3=x2-4,
解这个方程得:x2-4x+4-3-x2+4=0,
-4x=-5,
x=
 ,
,∵检验:把x=
 代入(x+2)(x-2)≠0,
代入(x+2)(x-2)≠0,∴x=
 是原方程的解.
是原方程的解.分析:(1)分别求出每一部分的值:sin30°=
 ,
,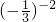 =9,
=9,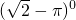 =1,
=1,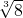 =2,(-1)2012=1,再代入求出即可;
=2,(-1)2012=1,再代入求出即可;(2)方程的两边乘以(x+2)(x-2)得出方程(x-2)(x-2)-3=x2-4,求出方程的解,在代入(x+2)(x-2)进行检验即可.
点评:本题考查了负指数幂,零指数幂,特殊角的三角函数值,解分式方程等知识点的应用,解(1)的关键是求出每一部分的值,解(2)的关键是把分式方程转化成整式方程,题目都较好,但是(1)小题是一道比较容易出错的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某几何体的三视图如图,则该几何体是
某几何体的三视图如图,则该几何体是 如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠BAD=40°,则∠C为
如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠BAD=40°,则∠C为

 已知:如图,BF⊥AC于点F,CE⊥AB于点E,且BD=CD
已知:如图,BF⊥AC于点F,CE⊥AB于点E,且BD=CD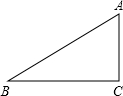 下图是深圳市“净畅宁”活动中拆除违章建筑后的一块三角形空地,已知△ABC中,∠C=90°,
下图是深圳市“净畅宁”活动中拆除违章建筑后的一块三角形空地,已知△ABC中,∠C=90°,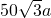 元
元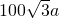 元
元 四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么tanθ的值是
四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为4,大正方形面积为74,直角三角形中较小的锐角为θ,那么tanθ的值是