题目内容
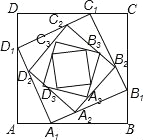
【题目】如图，正方形ABCD的边长为a，在AB、BC、CD、DA边上分别取点A1、B1、C1、D1，使AA1=BB1=CC1=DD1=
a，在边A1B1、B1C1，C1D1、D1A1上分别取点A2、B2、C2、D2，使A1A2、B1B2、C1C2、D1D2=A1B1，…，依次规律继续下去，则正方形AnBnCnDn的面积为（ ）
A．
B．（
）na2 C．（
）n-1a2 D．（）na2
【答案】D.
【解析】
试题解析：在Rt△A1BB1中，由勾股定理可知；A1B12=A1B2+B1B2=（
a）2+（
a）2=
a2，即正方形A1B1C1D1的面积=a2；
在Rt△A2B1B2中，由勾股定理可知：A2B22=A2B12+B2B12=（×
a）2+（×a）2=（）2a2；即正方形A2B2C2D2的面积=（）2a2；
…
∴正方形AnBnCnDn的面积=（）na2．
故选D．
练习册系列答案
相关题目
