题目内容
两个三角形中,三条边和三个角都对应相等,从中任取3个条件作为一组,能使两三角形全等的有组.
- A.10
- B.11
- C.12
- D.13
D
分析:分别找出符合条件SAS,ASA,AAS,SSS的组数,再相加即可得出答案.
解答: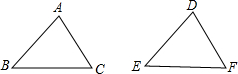
①AB=DE,②AC=DF,③BC=EF,④∠A=∠D,⑤∠E=∠B,⑥∠C=∠F,
满足全等三角形的判定定理SAS的有①②④,②③⑥,①③⑤,3组;
满足ASA的有④⑤①,⑥⑤③,④⑥②,3组;
满足AAS的有④⑤②,④⑤③,⑤⑥①,⑤⑥②,④⑥①,④⑥③,6组;
满足SSS的有①②③,1组,
共3+3+6+1=13,
故选D.
点评:本题考查了全等三角形的判定定理,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
分析:分别找出符合条件SAS,ASA,AAS,SSS的组数,再相加即可得出答案.
解答:
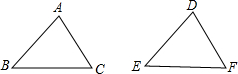
①AB=DE,②AC=DF,③BC=EF,④∠A=∠D,⑤∠E=∠B,⑥∠C=∠F,
满足全等三角形的判定定理SAS的有①②④,②③⑥,①③⑤,3组;
满足ASA的有④⑤①,⑥⑤③,④⑥②,3组;
满足AAS的有④⑤②,④⑤③,⑤⑥①,⑤⑥②,④⑥①,④⑥③,6组;
满足SSS的有①②③,1组,
共3+3+6+1=13,
故选D.
点评:本题考查了全等三角形的判定定理,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目