题目内容
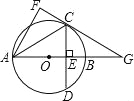
【题目】如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)直线FC与⊙O有何位置关系?并说明理由;
(2)若OB=BG=2,求CD的长.
【答案】(1)直线FC与⊙O相切.理由见试题解析;(2)CD=2CE=2![]()
【解析】
试题分析:(1)相切.连接OC,证OC⊥FG即可.根据题意AF⊥FG,证∠FAC=∠ACO可得OC∥AF,从而OC⊥FG,得证;
(2)根据垂径定理可求CE后求解.在Rt△OCG中,根据三角函数可得∠COG=60°.结合OC=2求CE,从而得解.
试题解析:(1)直线FC与⊙O相切.
理由如下:连接OC.
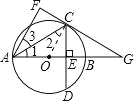
∵OA=OC,∴∠1=∠2.由翻折得,∠1=∠3,∠F=∠AEC=90°.∴∠2=∠3,∴OC∥AF.
∴∠OCG=∠F=90°.∴直线FC与⊙O相切.
(2)在Rt△OCG中,cos∠COG=![]() =
=![]() =
=![]() ,∴∠COG=60°.
,∴∠COG=60°.
在Rt△OCE中,CE=OC![]() 60°=2×
60°=2×![]() =
=![]() .∵直径AB垂直于弦CD,CD=2CE=2
.∵直径AB垂直于弦CD,CD=2CE=2![]() .
.

练习册系列答案
相关题目