题目内容
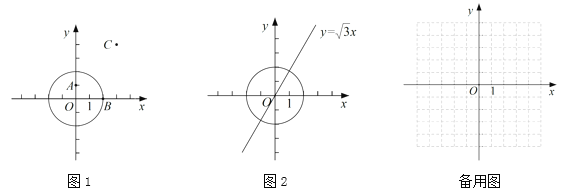
【题目】如图，在平面直角坐标系中，已知四个定点
、
、
、
，点
在四边形
内，则到四边形四个顶点的距离的和
最小时的点的坐标为______．
【答案】(-
，
)
【解析】
设AC与BD交于P′点，则由不等式的性质可得，PA+PC≥AC=P′A+P′C，PB+PD≥BD=P′B+P′D，得出PA+PB+PC+PD≥AC+BD，所以当P在P′处时PA+PB+PC+PD的值最小，再根据点P′为直线AC与BD的交点可求出此时点P′的坐标．
解：如图，设AC与BD交于P′点，则PA+PC≥AC=P′A+P′C，PB+PD≥BD=P′B+P′D，
因此，PA+PB+PC+PD≥AC+BD，当动点P在P′的位置时，PA+PB+PC+PD的值最小，
设直线AC的解析式为y=kx+b，将点A(-3，0)，C（0，3）代入得，
，解得
，∴直线AC的解析式为y=x+3①，
同理根据点B（1，-1），D（-1，3）可得直线BD的解析式为y=-2x+1②，
联立①②得，
，解得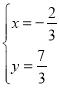
．
∴此时点P的坐标为：
．
故答案为：．
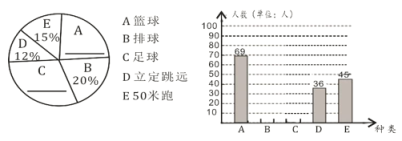
【题目】现今“微信运动”被越来越多的人关注和喜爱，某数学兴趣小组随机调查了我市
名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）：
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请根据以上信息，解答下列问题：
（1）写出
，
，
，
的值并补全频数分布直方图；
（2）我市约有
名教师，用调查的样本数据估计日行走步数超过
步（包含步）的教师有多少名？
（3）若在名被调查的教师中，选取日行走步数超过
步（包含步）的两名教师与大家分享心得，用树形图或列表法求被选取的两名教师恰好都在
步（包含步）以上的概率．
【题目】为了帮助市内一名患“白血病”的中学生，东营市某学校数学社团15名同学积极捐款，捐款情况如下表所示，下列说法正确的是（ ）
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
