题目内容
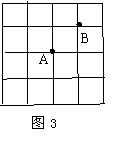
 如图,正方形网格在平面直角坐标系中,△ABC顶点C的坐标是(7,4),则△ABC外接圆的圆心坐标是________.
如图,正方形网格在平面直角坐标系中,△ABC顶点C的坐标是(7,4),则△ABC外接圆的圆心坐标是________.
(2,2)
分析:求出A、B的坐标,根据A、B的坐标求出O的横坐标,设O(2,a),根据OA=OC和勾股定理得出方程,求出方程的解即可.
解答:由图象可知A(0,8),B(4,8),
根据△ABC的外接圆的定义,圆心的横坐标是x=2,
设O(2,a),
根据勾股定理得:OA=OC,
82+22=52+(4-a)2
a=2,
∴O(2,2).
故答案为(2,2).
点评:本题主要考查对三角形的外接圆与外心,坐标与图形性质,勾股定理,垂径定理等知识点的理解和掌握,能根据题意得出O点的横坐标和得出方程是解此题的关键.
分析:求出A、B的坐标,根据A、B的坐标求出O的横坐标,设O(2,a),根据OA=OC和勾股定理得出方程,求出方程的解即可.
解答:由图象可知A(0,8),B(4,8),
根据△ABC的外接圆的定义,圆心的横坐标是x=2,
设O(2,a),
根据勾股定理得:OA=OC,
82+22=52+(4-a)2
a=2,
∴O(2,2).
故答案为(2,2).
点评:本题主要考查对三角形的外接圆与外心,坐标与图形性质,勾股定理,垂径定理等知识点的理解和掌握,能根据题意得出O点的横坐标和得出方程是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目