题目内容
在测量某物理量的过程中，因为仪器和观察的误差，使得n次测量分别得到a1，a2，…，an共n个数据，我们规定所测得的物理量的“最佳近似值”a是这样一个数据：与其他近似值比较，a与各个数据差的平方和最小．若四次测量得到的数据依次为3、5、6，10依据此规定，那么本次测量的“最佳近似值”为（ ）
分析：由题意知所测量的“量佳近似值”a是与其他近似值比较，a与各数据的差的平方和最小．根据均值不等式求平方和的最小值知这些数的底数要尽可能的接近，知a是所有数字的平均数．
解答：解：∵所测量的“量佳近似值”a是与其他近似值比较，
a与各数据的差的平方和最小．
根据平均值不等式求平方和的最小值知这些数的底数要尽可能的接近，
∴a是所有数字的平均数，
∴a=（3+5+6+10）÷4=6；
故选：B．
a与各数据的差的平方和最小．
根据平均值不等式求平方和的最小值知这些数的底数要尽可能的接近，
∴a是所有数字的平均数，
∴a=（3+5+6+10）÷4=6；
故选：B．
点评：此题考查了一组数据的方差、平均数，考查平均数的平方和最小时要满足的条件，是一个基础题，没有运算，只有理论说明．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
次测量分别得到
共
是这样一个数据：与其他近似值比较，
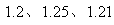，依据此规定，那么本次测量的“最佳近似值”为（
）