题目内容
【题目】如图,△ABC内接于⊙O,AB、CD为⊙O直径,DE⊥AB于点E,sinA= ![]() ,则∠D的度数是 .
,则∠D的度数是 . 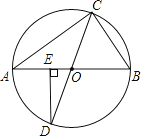
【答案】30°
【解析】解:∵AB为⊙O直径,
∴∠ACB=90°(直径所对的圆周角是直角);
又∵sinA= ![]() ,
,
∴∠CAB=30°,
∴∠ABC=60°(直角三角形的两个锐角互余);
又∵点O是AB的中点,
∴OC=OB,
∴∠OCB=OBC=60°,
∴∠COB=60°,
∴∠EOD=∠COB=60°(对顶角相等);
又∵DE⊥AB,
∴∠D=90°﹣60°=30°.
故答案是:30°.
由圆周角定理、特殊角的三角函数值求得∠CAB=30°;然后根据直角三角形的两个锐角互余的性质、等腰三角形的性质、对顶角相等求得∠EOD=∠COB=60°;最后在直角三角形ODE中求得∠D的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元