题目内容
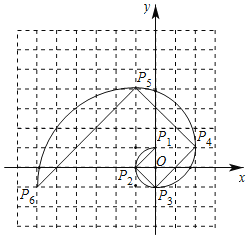
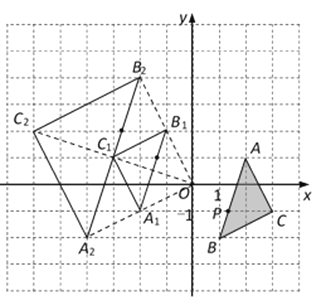
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,1),B(1,-2),C(3,-1),P(m,n)是△ABC的边AB上一点.
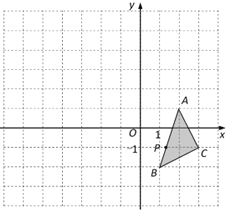
(1)画出△A1B1C1,使△A1B1C1与△ABC关于点O成中心对称,并写出点A、P的对应点A1、P1的坐标.
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出将△A1B1C1放大后的△A2B2C2,并分别写出点A1、P1的对应点A2、P2的坐标.
(3)求sin∠B2A2C2的值.
【答案】(1)画图见解析;A1(-2,-1),P1(-m,-n);(2)画图见解析,A2(-4,-2),P2(-2m,-2n);(3)sin∠B2A2C2=![]() .
.
【解析】
(1)作出△ABC各点关于原点的对称点,再顺次连接,再根据原点对称图形性质求出A1、P1的坐标;
(2)利用位似图形的性质得出对应点位置即可得出答案;
(3)证实△ABC为等腰直角三角形及△ABC和△A2 B2C2相似即可求出结果.
解:(1)如图,A1(-2,-1),P1(-m,-n);
(2)如图,A2(-4,-2),P2(-2m,-2n);
(3) ∵AC=![]() ,BC=
,BC=![]() ,AB=
,AB=![]() ,
,
∴![]() ,AC=BC
,AC=BC
∴△ABC为等腰直角三角形,
又∵△ABC和△A1B1C1关于原点对称,△A1B1C1和△A2 B2C2相似,
∴△ABC和△A2 B2C2相似,△A2 B2C2是等腰直角三角形,
∴ sin∠B2A2C2= sin45°=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目