ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊжБЯп![]() ЃЌЧв
ЃЌЧв![]() КЭ
КЭ![]() жЎМфЕФОрРыЮЊ
жЎМфЕФОрРыЮЊ![]() ЃЌаЁУїЭЌбЇжЦзїСЫвЛИіжБНЧШ§НЧаЮгВжНАх
ЃЌаЁУїЭЌбЇжЦзїСЫвЛИіжБНЧШ§НЧаЮгВжНАх![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .аЁУїРћгУетПщШ§НЧАхНјааСЫШчЯТЕФВйзїЬНОПЃК
.аЁУїРћгУетПщШ§НЧАхНјааСЫШчЯТЕФВйзїЬНОПЃК
(1)ШчЭМ1ЃЌШєЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() .Чѓ
.Чѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
(2)ШєЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дк
дк![]() КЭ
КЭ![]() жЎМф(ВЛКЌ
жЎМф(ВЛКЌ![]() ЁЂ
ЁЂ![]() ЩЯ)ЃЌБп
ЩЯ)ЃЌБп![]() ЁЂ
ЁЂ![]() гыжБЯп
гыжБЯп![]() ЗжБ№НЛгкЕу
ЗжБ№НЛгкЕу![]() КЭЕу
КЭЕу![]() .
.
ЂйШчЭМ2ЃЌ![]() ЁЂ
ЁЂ![]() ЕФЦНЗжЯпНЛгкЕу
ЕФЦНЗжЯпНЛгкЕу![]() .дк
.дк![]() ШЦзХЕу
ШЦзХЕу![]() а§зЊЕФЙ§ГЬжаЃЌ
а§зЊЕФЙ§ГЬжаЃЌ![]() ЕФЖШЪ§ЪЧЗёБфЛЏЃПШєВЛБфЃЌЧѓГі
ЕФЖШЪ§ЪЧЗёБфЛЏЃПШєВЛБфЃЌЧѓГі![]() ЕФЖШЪ§ЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛ
ЕФЖШЪ§ЃЛШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛ
ЂкШчЭМ3ЃЌдк![]() ШЦзХЕу
ШЦзХЕу![]() а§зЊЕФЙ§ГЬжаЃЌЩш
а§зЊЕФЙ§ГЬжаЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖ
ЕФШЁжЕЗЖ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЂйВЛБфЃЌ
ЃЛЃЈ2ЃЉЂйВЛБфЃЌ![]() ЃЛЂк
ЃЛЂк![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнСНжБЯпЦНааЃЌФкДэНЧЯрЕШПЩЕУЁЯ1ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЂйЯШИљОнЫФБпаЮЕФФкНЧКЭЕУЁЯAKD+ЁЯCDK=360Ёу-90Ёу-60Ёу=210ЁуЃЌгЩНЧЦНЗжЯпЕФЖЈвхКЭШ§НЧаЮЕФФкНЧКЭПЩЕУНсТлЃЛ
ЂкЯШИљОнЂйЕФНсТлЃЌНсКЯЦНааЯпЕФаджЪЕУЃКn=2m-110ЃЌШЗШЯЕуCБпНчЩЯСНЕуЪБЃЌnЕФШЁжЕЃЌДњШыn=2m-110ЃЌПЩЕУНсТлЃЎ
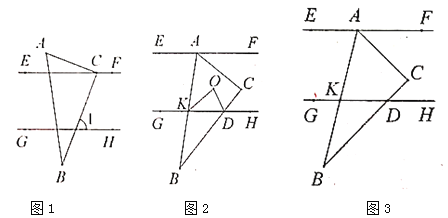
ЃЈ1ЃЉШчЭМ1ЃЌЁпЁЯACB=90ЁуЃЌЁЯACE=20ЁуЃЌ
ЁрЁЯECB=90Ёу-20Ёу=70ЁуЃЌ
ЁпEFЁЮGHЃЌ
ЁрЁЯ1=ЁЯECB=70ЁуЃЛ

ЃЈ2ЃЉЂйдкЁїABCШЦзХЕуAа§зЊЕФЙ§ГЬжаЃЌЁЯOЕФЖШЪ§ВЛЗЂЩњБфЛЏЃЌ
РэгЩЪЧЃКШчЭМ2ЃЌ

ЁпЁЯBAC=60ЁуЃЌЁЯACB=90ЁуЃЌ
ЁрЁЯAKD+ЁЯCDK=360Ёу-90Ёу-60Ёу=210ЁуЃЌ
ЁпЁЯAKDЁЂЁЯCDKЕФЦНЗжЯпНЛгкЕуOЃЌ
ЁрЁЯOKD=![]() ЁЯAKDЃЌЁЯODK=
ЁЯAKDЃЌЁЯODK=![]() ЁЯCDKЃЌ
ЁЯCDKЃЌ
ЁрЁЯOKD+ЁЯODK=105ЁуЃЌ
ЁрЁЯO=180Ёу-105Ёу=75ЁуЃЛ
ЂкЁпEFЁЮGHЃЌ
ЁрЁЯEAK=ЁЯAKD=nЁуЃЌ
гЩЂйжЊЃКЁЯAKD+ЁЯCDK=210ЁуЃЌ
Ёрn+4m-3n-10=210ЃЌ
n=2m-110ЃЌ
ШчЭМ3ЃЌЕуCдкжБЯпEFЩЯЪБЃЌЁЯEAK=n=180Ёу-60Ёу=120ЁуЃЌ

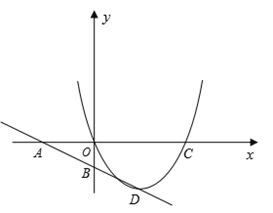
ШчЭМ4ЃЌЁпAC=1ЃЌЧвEFКЭGHжЎМфЕФОрРыЮЊ1ЃЌ
ЁрЕуCдкжБЯпGHЩЯЪБЃЌЁЯEAK=n=90Ёу-60Ёу=30ЁуЃЌ

ЁпЕуCдкEFКЭGHжЎМфЃЈВЛКЌEFЁЂGHЩЯЃЉЃЌ
Ёр30ЁуЃМnЃМ120ЁуЃЌ
МД30ЃМ2m-110ЃМ120ЃЌ
ЁрmЕФШЁжЕЗЖЮЇЪЧЃК70ЁуЃМmЃМ115ЁуЃЎ

 еуНУћаЃУћЪІН№ОэЯЕСаД№АИ
еуНУћаЃУћЪІН№ОэЯЕСаД№АИ ШЋгХГхДЬ100ЗжЯЕСаД№АИ
ШЋгХГхДЬ100ЗжЯЕСаД№АИ