题目内容
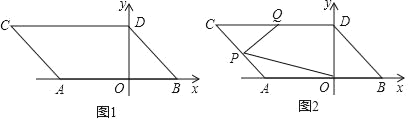
【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|2a+6|+(2a﹣3b+12)2=0,现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)请直接写出A,B两点的坐标;
(2)如图2,点P是线段AC上的一个动点,点Q是线段CD的中点,连接PQ,PO,当点P在线段AC上移动时(不与A,C重合),请找出∠PQD,∠OPQ,∠POB的数量关系,并证明你的结论;
(3)在坐标轴上是否存在点M,使三角形MAD的面积与三角形ACD的面积相等?若存在,直接写出点M的坐标;若不存在,试说明理由.
【答案】(1)A(﹣3,0),B(2,0);(2)∠PQD+∠OPQ+∠POB=360°,理由见解析;(3)三角形MAD的面积与三角形ACD的面积相等时,点M的坐标为(2,0)或(﹣8,0)或(0,﹣![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)根据绝对值的非负性、偶次方的非负性分别求出a、b,得到点A,B的坐标;
(2)求出五边形QPOBD的内角和,根据平行线的性质得到∠QDB+∠OBD=180°,计算即可;
(3)根据题意求出△ACD的面积,分点M在x轴上、点M在y轴上两种情况,根据三角形的面积公式计算即可.
解:(1)∵|2a+6|+(2a﹣3b+12)2=0,
∴|2a+6|=0,(2a﹣3b+12)2=0,
解得,a=﹣3,b=2,
则点A,B的坐标分别为A(﹣3,0),B(2,0);
(2)∠PQD+∠OPQ+∠POB=360°,
理由如下:五边形QPOBD的内角和=(5﹣2)×180°=540°,
∵CD∥AB,
∴∠QDB+∠OBD=180°,
∴∠PQD+∠OPQ+∠POB=540°﹣(∠QDB+∠OBD)=360°;
(3)由题意得,点C的坐标为(﹣5,2),点D的坐标为(0,2),
则△ACD的面积=![]() ×5×2=5,
×5×2=5,
当点M在x轴上时,设点M的坐标为(x,0),
则AM=|﹣3﹣x|,
由题意得,![]() ×|﹣3﹣x|×2=5,
×|﹣3﹣x|×2=5,
解得,x=2或﹣8,
当点M在y轴上时,设点M的坐标为(0,y),
则AM=|2﹣y|,
由题意得,![]() ×|2﹣y|×3=5,
×|2﹣y|×3=5,
解得,y=﹣![]() 或
或![]() ,
,
综上所述,三角形MAD的面积与三角形ACD的面积相等时,点M的坐标为(2,0)或(﹣8,0)或(0,﹣![]() )或(0,
)或(0,![]() ).
).

【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现,优秀漏统计![]() 人,良好漏统计
人,良好漏统计![]() 人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生![]() 人,请你估算出该校体能测试等级为“优秀”的人数.
人,请你估算出该校体能测试等级为“优秀”的人数.
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 |
| |
良好 |
| |
及格 |
| |
不及格 |
| |
合计 |
|
学生体能测试成绩各等次人数统计图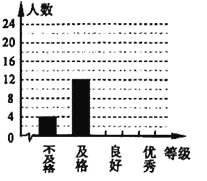
【题目】如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层。第二层……第n层,第n层的小正方体的个数记为S.解答下列问题:
(1)填写表格:
n | 1 | 2 | 3 | 4 | … |
S | 1 |
| … |
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?