题目内容
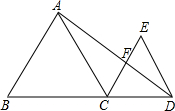 如图所示,C在BD上,且BC=3,CD=2,△ABC,△ECD均为等边三角形,AD与CE交于F,则△ACF的周长:△EDF的周长的值为
如图所示,C在BD上,且BC=3,CD=2,△ABC,△ECD均为等边三角形,AD与CE交于F,则△ACF的周长:△EDF的周长的值为
- A.4:3
- B.9:5
- C.9:4
- D.3:2
D
分析:根据△ABC,△ECD均为等边三角形,可知∠ACB=∠ECD=∠CED=60°,结合平角定义易求∠ACE=60°,那么∠ACF=∠DEF,而∠ACF=∠DEF,可证△AFC∽△DFE,根据相似三角形的周长比等于相似比可求△ACF的周长:△EDF的周长.
解答: ∵△ABC,△ECD均为等边三角形,
∵△ABC,△ECD均为等边三角形,
∴∠ACB=∠ECD=∠CED=60°,
∴∠ACE=180°-∠ACB-∠ECD=180°-60°-60°=60°,
∴∠ACF=∠DEF,
又∵∠AFC=∠DFE,
∴△AFC∽△DFE,
∴△ACF的周长:△EDF的周长=AC:ED=3:2.
故选D.
点评:本题考查了等边三角形的性质,相似三角形的判定和性质,解题的关键是证明△AFC∽△DFE.
分析:根据△ABC,△ECD均为等边三角形,可知∠ACB=∠ECD=∠CED=60°,结合平角定义易求∠ACE=60°,那么∠ACF=∠DEF,而∠ACF=∠DEF,可证△AFC∽△DFE,根据相似三角形的周长比等于相似比可求△ACF的周长:△EDF的周长.
解答:
 ∵△ABC,△ECD均为等边三角形,
∵△ABC,△ECD均为等边三角形,∴∠ACB=∠ECD=∠CED=60°,
∴∠ACE=180°-∠ACB-∠ECD=180°-60°-60°=60°,
∴∠ACF=∠DEF,
又∵∠AFC=∠DFE,
∴△AFC∽△DFE,
∴△ACF的周长:△EDF的周长=AC:ED=3:2.
故选D.
点评:本题考查了等边三角形的性质,相似三角形的判定和性质,解题的关键是证明△AFC∽△DFE.

练习册系列答案
相关题目
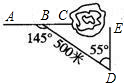 如图所示,施工队在沿AC方向开山修路,为了加快施工进度,要在小山的另一边点E同时施工,从AC上的一点B,取∠ABD=145°,BD=500米,∠D=55°,要使A,C,E成一直线,那么开挖点E离点B的距离如何求得?请你设计出解决方案.
如图所示,施工队在沿AC方向开山修路,为了加快施工进度,要在小山的另一边点E同时施工,从AC上的一点B,取∠ABD=145°,BD=500米,∠D=55°,要使A,C,E成一直线,那么开挖点E离点B的距离如何求得?请你设计出解决方案. 如图所示,C在BD上,且BC=3,CD=2,△ABC,△ECD均为等边三角形,AD与CE交于F,则△ACF的周长:△EDF的周长的值为( )
如图所示,C在BD上,且BC=3,CD=2,△ABC,△ECD均为等边三角形,AD与CE交于F,则△ACF的周长:△EDF的周长的值为( )
