题目内容
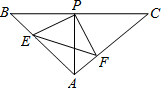
 如图所示△ABC中,AB=AC,AE=AF,连BF,CE交于K,连AK并延长AK交于D,DE与BF交于G,DF与CE交于H,则图中全等三角形的对数为( )
如图所示△ABC中,AB=AC,AE=AF,连BF,CE交于K,连AK并延长AK交于D,DE与BF交于G,DF与CE交于H,则图中全等三角形的对数为( )分析:先根据边角边证明△ABF与△ACE全等,根据全等三角形对应角相等可得∠ABF=∠ACE,再根据等边对等角可得∠ABC=∠ACB,从而求出∠KBD=∠KCD,然后根据等角对等边的性质得到BK=CK,从而证明图形关于直线AD成轴对称,再根据轴对称的性质找出所有的全等三角形即可得解.
解答:解:在△ABF与△ACE中,
,
∴△ABF≌△ACE(SAS),
∴∠ABF=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC-∠ABF=∠ACB-∠ACE,
即∠KBD=∠KCD,
∴BK=CK,
∴图形关于直线AD成轴对称,
∴全等的三角形有:△BDG≌△CDH,△DGK≌△DHK,△BGE≌△CHF,△EGK≌△FHK,△AEK≌△AFK,(5对)
△BDK≌△CDK,△BDE≌△CDF,△BEK≌△CFK,△DEK≌△DFK,△ABK≌△ACK,△ADE≌△ADF,△ABD≌△ACD,(7对)
△ABF≌△ACE,△BDF≌△CDE,△BCE≌△CBF,△DEH≌△DFG,(4对).
共16对.
故选C.
|
∴△ABF≌△ACE(SAS),
∴∠ABF=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC-∠ABF=∠ACB-∠ACE,
即∠KBD=∠KCD,
∴BK=CK,
∴图形关于直线AD成轴对称,
∴全等的三角形有:△BDG≌△CDH,△DGK≌△DHK,△BGE≌△CHF,△EGK≌△FHK,△AEK≌△AFK,(5对)
△BDK≌△CDK,△BDE≌△CDF,△BEK≌△CFK,△DEK≌△DFK,△ABK≌△ACK,△ADE≌△ADF,△ABD≌△ACD,(7对)
△ABF≌△ACE,△BDF≌△CDE,△BCE≌△CBF,△DEH≌△DFG,(4对).
共16对.
故选C.
点评:本题主要考查等腰三角形的性质,全等三角形的判定及性质,图形中的三角形较多,关键在于按照一定的顺序找出全等的三角形.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 B、AC于点E、F,给出以下四个结论:
B、AC于点E、F,给出以下四个结论: 如图所示△ABC中,已知DE∥BC,AD=3BD,S△ABC=48,则S△ADE=
如图所示△ABC中,已知DE∥BC,AD=3BD,S△ABC=48,则S△ADE=
