题目内容
(2004•呼和浩特)将下列式子因式分解:x-x2-y+y2=
(x-y)(1-x-y)
(x-y)(1-x-y)
.分析:将原式进一步整理为(x-y)-(x2-y2),再将第二项利用平方差公式分解后提取公因式x-y即可.
解答:解:原式=(x-y)-(x2-y2)
=(x-y)-(x+y)(x-y)
=(x-y)(1-x-y),
故答案为:(x-y)(1-x-y).
=(x-y)-(x+y)(x-y)
=(x-y)(1-x-y),
故答案为:(x-y)(1-x-y).
点评:本题考查了分组分解法因式分解的知识,解题的关键是将原式正确的分组并利用正确的添加括号.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
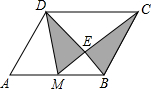 (2004•呼和浩特)如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是( )
(2004•呼和浩特)如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是( )