Question

梯形的面积被一条对角线分成1：2两部分，则梯形的中位线分梯形的两部分面积之比为

 

．

Answer 1

分析：根据题意先求上下两底的关系，再根据梯形的中位线定理求解．

解答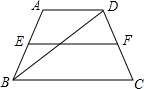：解：设上底长x，下底y，中位线z．
梯形的面积被一条对角线分成1：2，因为两部分的高相等，所以

x

y

=

1

2

，z=

x+2x

2

=

3

2

x．
根据中位线的性质中位线分成两部分的梯形同高

x+ 3x 2

2

÷（

3x

2

+2x）=

5

7

．

点评：本题为中等难度题，在解此类题目时一定要找到“等高”这一突破口解答．