题目内容
如图,⊙O的半么为6,AB为弦,将⊙O沿弦AB所在的直线折叠后,
上的点H与圆心O重合.
(1)求弦AB的长度.
(2)点E是
上的动点,过点E作
的切线交⊙O于C、D两点.
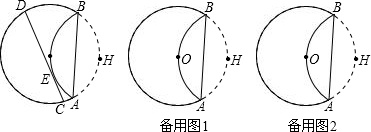
①当点E与点O重合时,判断CD与AB的位置关系,并说明理由;
②当点C与点A重合时,判断CD与AB的数量关系,并说明理由;
③请你直接写出线段CD的长度的范围.
 |
| AB |
(1)求弦AB的长度.
(2)点E是
 |
| AOB |
 |
| AOB |
①当点E与点O重合时,判断CD与AB的位置关系,并说明理由;
②当点C与点A重合时,判断CD与AB的数量关系,并说明理由;
③请你直接写出线段CD的长度的范围.

分析:(1)连接EH,BO,根据勾股定理求出BM,根据垂径定理求出AB=2BM,求出即可;
(2)①连接EH,根据折叠得出AB⊥OH,根据切线定理得出HO⊥CD,根据平行线的判定推出即可;②求出AD长,即可得出答案;③当和A或B重合时,CD=AB,当和A、B不重合时,根据直径是最长的弦,CD>6
.
(2)①连接EH,根据折叠得出AB⊥OH,根据切线定理得出HO⊥CD,根据平行线的判定推出即可;②求出AD长,即可得出答案;③当和A或B重合时,CD=AB,当和A、B不重合时,根据直径是最长的弦,CD>6
| 3 |
解答:解:(1)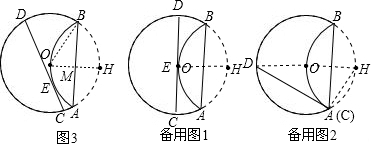 如图3,连接EH,BO,
如图3,连接EH,BO,
∵⊙O半径为6,沿AB折叠H和O重合,
∴OM=HM=3,OH⊥AB,
∴由垂径定理得:AB=2BM=2AM,由勾股定理得:BM=
=3
,
即AB=6
;
(2)①当点E与点O重合时,CD∥AB,
理由是:如图1,连接HE,
∵OH是半径,CD切⊙H于E,
∴OH⊥CD,
∵OH⊥AB,
∴CD∥AB;
②如图2,当点C与点A重合时,CD=AB=6
,
理由是:连接HD,
∵CD切⊙H于A,
∴HA⊥CD,
∴∠HAD=90°,
∴HD为直径,
即HD=2×6=12,
∵AH=6,
∴在Rt△DAH中,AD=
=6
,
即CD=AB=6
;
③∵当和A或B重合时,CD=AB,当和A、B不重合时,根据直径是最长的弦,CD>6
,
∴线段CD的长度的范围是CD≥6
.
 如图3,连接EH,BO,
如图3,连接EH,BO,∵⊙O半径为6,沿AB折叠H和O重合,
∴OM=HM=3,OH⊥AB,
∴由垂径定理得:AB=2BM=2AM,由勾股定理得:BM=
| 62-32 |
| 3 |
即AB=6
| 3 |
(2)①当点E与点O重合时,CD∥AB,
理由是:如图1,连接HE,
∵OH是半径,CD切⊙H于E,
∴OH⊥CD,
∵OH⊥AB,
∴CD∥AB;
②如图2,当点C与点A重合时,CD=AB=6
| 3 |
理由是:连接HD,
∵CD切⊙H于A,
∴HA⊥CD,
∴∠HAD=90°,
∴HD为直径,
即HD=2×6=12,
∵AH=6,
∴在Rt△DAH中,AD=
| 122-62 |
| 3 |
即CD=AB=6
| 3 |
③∵当和A或B重合时,CD=AB,当和A、B不重合时,根据直径是最长的弦,CD>6
| 3 |
∴线段CD的长度的范围是CD≥6
| 3 |
点评:本题考查了切线性质,垂径定理,勾股定理,平行线性质和判定的应用,注意:直径是最长的弦.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
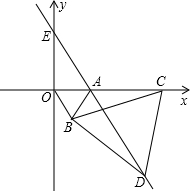 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连结BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连结BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.