题目内容
作一个辅助圆证明：△ABC中，若AD平分∠A，则| AB |
| AC |
| BD |
| DC |
（提示：不妨设AB≥AC，作△ADC的外接圆交AB于E，证△ABC∽△DBE，从而
| AB |
| AC |
| BD |
| DE |
| BD |
| DC |
分析：如图，作△ADC的外接圆O，交AB于E，连接DE，根据圆内接四边形的外角等于内对角的性质可知∠BED=∠C，可证△ABC∽△DBE，从而有
=
，再根据圆周角∠EAD=∠CAD可得DE=DC，可证结论．
| AB |
| AC |
| BD |
| DE |
解答：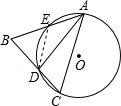
证明：如图，作△ADC的外接圆O，交AB于E，连接DE，
∵四边形ACDE为圆内接四边形，
∴∠BED=∠C，
又∠ABC=∠DBE，
∴△ABC∽△DBE，
∴
=
，
又∵∠EAD=∠CAD，
∴DE=DC，
∴
=
．
证明：如图，作△ADC的外接圆O，交AB于E，连接DE，∵四边形ACDE为圆内接四边形，
∴∠BED=∠C，
又∠ABC=∠DBE，
∴△ABC∽△DBE，
∴
| AB |
| AC |
| BD |
| DE |
又∵∠EAD=∠CAD，
∴DE=DC，
∴
| AB |
| AC |
| BD |
| DC |
点评：本题考查了圆内接四边形的性质，相似三角形的判定与性质，圆周角定理的综合运用，解题时，需要灵活把握．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
=
．
=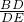