题目内容
 宏达广告公司设计员刘斌在设计一个广告图案,他先在纸上画了一个边长为1分米的正六边形,然后连接相隔一点的两顶点得到如图所示的对称图案.他发现中间也出现了一个正六边形,则中间的正六边形的面积是
宏达广告公司设计员刘斌在设计一个广告图案,他先在纸上画了一个边长为1分米的正六边形,然后连接相隔一点的两顶点得到如图所示的对称图案.他发现中间也出现了一个正六边形,则中间的正六边形的面积是
- A.
 分米2
分米2 - B.
 分米2
分米2 - C.
 分米2
分米2 - D.
 分米2
分米2
C
分析:根据连接相隔一点的两顶点得到如图所示的对称图案,得出QO=0.5分米,进而利用勾股定理得出MO= ×2=
×2= 分米,即可得出S△MON以及中间的正六边形的面积.
分米,即可得出S△MON以及中间的正六边形的面积.
解答: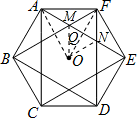 解:连接NO,MO,设FO与AE交于点Q,
解:连接NO,MO,设FO与AE交于点Q,
∵一个边长为1分米的正六边形,连接相隔一点的两顶点得到如图所示的对称图案,
∴AF=FO=AO=1分米,
∴QO=0.5分米,
∴设MQ=x,MO=2x,
∴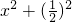 =(2x)2,
=(2x)2,
解得:x= ,
,
∴MO= ×2=
×2= 分米,
分米,
∴S△MON= ×MN×QO=
×MN×QO= ×
× ×
× =
=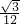 平方分米,
平方分米,
∴中间的正六边形的面积是:6×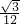 =
= 平方分米,
平方分米,
故选:C.
点评:此题主要考查了正多边形的性质以及勾股定理等知识,根据已知得出MO=MN的长是解题关键.
分析:根据连接相隔一点的两顶点得到如图所示的对称图案,得出QO=0.5分米,进而利用勾股定理得出MO=
 ×2=
×2= 分米,即可得出S△MON以及中间的正六边形的面积.
分米,即可得出S△MON以及中间的正六边形的面积.解答:
 解:连接NO,MO,设FO与AE交于点Q,
解:连接NO,MO,设FO与AE交于点Q,∵一个边长为1分米的正六边形,连接相隔一点的两顶点得到如图所示的对称图案,
∴AF=FO=AO=1分米,
∴QO=0.5分米,
∴设MQ=x,MO=2x,
∴
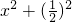 =(2x)2,
=(2x)2,解得:x=
 ,
,∴MO=
 ×2=
×2= 分米,
分米,∴S△MON=
 ×MN×QO=
×MN×QO= ×
× ×
× =
=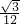 平方分米,
平方分米,∴中间的正六边形的面积是:6×
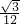 =
= 平方分米,
平方分米,故选:C.
点评:此题主要考查了正多边形的性质以及勾股定理等知识,根据已知得出MO=MN的长是解题关键.

练习册系列答案
相关题目