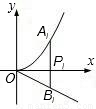
题目内容
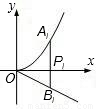
如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交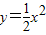 的图象于点Ai,交直线
的图象于点Ai,交直线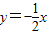 于点Bi.则
于点Bi.则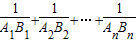 = .
= .
【答案】分析:根据函数图象上的坐标的特征求得A1(1, )、A2(2,2)、A3(3,
)、A2(2,2)、A3(3, )…An(n,
)…An(n, n2);B1(1,-
n2);B1(1,- )、B2(2,-1)、B3(3,-
)、B2(2,-1)、B3(3,- )…Bn(n,-
)…Bn(n,- );然后由两点间的距离公式求得A1B1=|
);然后由两点间的距离公式求得A1B1=| -(-
-(- )|=1,A2B2=|2-(-1)|=3,A3B3=|
)|=1,A2B2=|2-(-1)|=3,A3B3=| -(-
-(- )|=6,…AnBn=|
)|=6,…AnBn=| n2-(-
n2-(-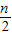 )|=
)|= ;最后将其代入
;最后将其代入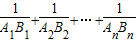 求值即可.
求值即可.
解答:解:根据题意,知A1、A2、A3、…An的点都在函与直线x=i(i=1、2、…、n)的图象上,
B1、B2、B3、…Bn的点都在直线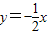 与直线x=i(i=1、2、…、n)图象上,
与直线x=i(i=1、2、…、n)图象上,
∴A1(1, )、A2(2,2)、A3(3,
)、A2(2,2)、A3(3, )…An(n,
)…An(n, n2);
n2);
B1(1,- )、B2(2,-1)、B3(3,-
)、B2(2,-1)、B3(3,- )…Bn(n,-
)…Bn(n,-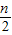 );
);
∴A1B1=| -(-
-(- )|=1,
)|=1,
A2B2=|2-(-1)|=3,
A3B3=| -(-
-(- )|=6,
)|=6,
…
AnBn=| n2-(-
n2-(- )|=
)|= ;
;
∴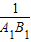 =1,
=1,
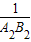 =
= ,
,
…
 =
= .
.
∴ ,
,
=1+ +
+ …+
…+ ,
,
=2[ +
+ +
+ +…+
+…+ ],
],
=2(1- +
+ -
- +
+ -
- +…+
+…+ -
- ),
),
=2(1-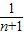 ),
),
= .
.
故答案为: .
.
点评:本题考查了二次函数的综合题.解答此题的难点是求 =1+
=1+ +
+ …+
…+ 的值.在解时,采取了“裂项法”来求该数列的和.
的值.在解时,采取了“裂项法”来求该数列的和.
 )、A2(2,2)、A3(3,
)、A2(2,2)、A3(3, )…An(n,
)…An(n, n2);B1(1,-
n2);B1(1,- )、B2(2,-1)、B3(3,-
)、B2(2,-1)、B3(3,- )…Bn(n,-
)…Bn(n,- );然后由两点间的距离公式求得A1B1=|
);然后由两点间的距离公式求得A1B1=| -(-
-(- )|=1,A2B2=|2-(-1)|=3,A3B3=|
)|=1,A2B2=|2-(-1)|=3,A3B3=| -(-
-(- )|=6,…AnBn=|
)|=6,…AnBn=| n2-(-
n2-(-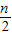 )|=
)|= ;最后将其代入
;最后将其代入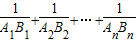 求值即可.
求值即可.解答:解:根据题意,知A1、A2、A3、…An的点都在函与直线x=i(i=1、2、…、n)的图象上,
B1、B2、B3、…Bn的点都在直线
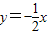 与直线x=i(i=1、2、…、n)图象上,
与直线x=i(i=1、2、…、n)图象上,∴A1(1,
 )、A2(2,2)、A3(3,
)、A2(2,2)、A3(3, )…An(n,
)…An(n, n2);
n2);B1(1,-
 )、B2(2,-1)、B3(3,-
)、B2(2,-1)、B3(3,- )…Bn(n,-
)…Bn(n,-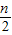 );
);∴A1B1=|
 -(-
-(- )|=1,
)|=1,A2B2=|2-(-1)|=3,
A3B3=|
 -(-
-(- )|=6,
)|=6,…
AnBn=|
 n2-(-
n2-(- )|=
)|= ;
;∴
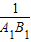 =1,
=1,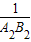 =
= ,
,…
 =
= .
.∴
 ,
,=1+
 +
+ …+
…+ ,
,=2[
 +
+ +
+ +…+
+…+ ],
],=2(1-
 +
+ -
- +
+ -
- +…+
+…+ -
- ),
),=2(1-
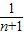 ),
),=
 .
.故答案为:
 .
.点评:本题考查了二次函数的综合题.解答此题的难点是求
 =1+
=1+ +
+ …+
…+ 的值.在解时,采取了“裂项法”来求该数列的和.
的值.在解时,采取了“裂项法”来求该数列的和. 
练习册系列答案
相关题目
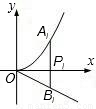
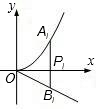 如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交
如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交 如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交
如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交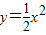 的图象于点Ai,交直线
的图象于点Ai,交直线 于点Bi.则
于点Bi.则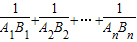 = .
= .
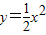 的图象于点Ai,交直线
的图象于点Ai,交直线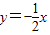 于点Bi.则
于点Bi.则 = .
= .