题目内容

若m、n满足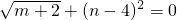 $数学公式$ ，分解因式：（x²+y²）-（mxy+n）．

解：由题意，得 $\text{[math]}$ ，
解得m=-2，n=4．
∴（x²+y²）-（-mxy+n），
=x²+y²-（-2xy+4），
=x²+y²+2xy-4，
=（x+y）²-4，
=（x+y+2）（x+y-2）．
分析：首先根据非负数的性质求出m、n的值，代入式子，然后利用分组分解法进行分解．
点评：本题考查用分组分解法进行因式分解．难点是采用两两分组还是三一分组．

练习册系列答案

中考1对1全程精讲导练系列答案

中考备考全攻略系列答案

中考一卷通系列答案

指南针神州中考系列答案

中考冲刺系列答案

中考特训营真题分类集训系列答案

中考先锋系列答案

中考真题分类卷系列答案

中考智胜考典系列答案

中考总复习导与练系列答案

相关题目

3、若多项式x²+kx-18分解因式的结果为（x+2）（x-m），则（k+m）的值为（　　）

（2013•清远模拟）若把多项式x²+px+q分解因式可以分解成（x-3）（x+5），则p的值是（　　）

先阅读下面例题的解法，然后解答后面的问题．
例：若多项式2x³-x²+m分解因式的结果中有因式2x+1，求实数m的值．
解：设2x³-x²+m=（2x+1）•A   （A为整数）
    若2x³-x²+m=（2x+1）•A=0，则2x+1=0或A=0
    由2x+1=0得x=-

是方程2x³-x²+m=0的解
所以2×（-

）²+m=0，即-

+m=0，所以m=

问题：
（1）若多项式x²+px-6分解因式的结果中有因式x-3，则实数P=

；
（2）若多项式x³+5x²+7x+q分解因式的结果中有因式x+1，求实数q的值；
（3）若多项式x⁴+mx³+nx-16分解因式的结果中有因式（x-1）和（x-2），求实数m、n的值．

，分解因式：(x²+y²)-(mxy+n)。