题目内容
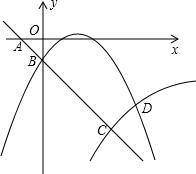 如图,在平面直角坐标系中,直线y=-x-1分别交x轴、y轴于点A、点B,交双曲线于点C(3,n).抛物线y=ax2+
如图,在平面直角坐标系中,直线y=-x-1分别交x轴、y轴于点A、点B,交双曲线于点C(3,n).抛物线y=ax2+| 3 |
| 2 |
(1)求该双曲线与抛物线的解析式;
(2)若点P为该抛物线上一点,点Q为该双曲线上一点,且P、Q两点的纵坐标都为-2,求线段PQ的长;
(3)若点M沿直线从点A运动到点C,再沿双曲线从点C运动到点D,过点M作MN⊥x轴,交抛物线于点N.设线段MN的长度为d,点M的横坐标为m,直接写出d的最大值,以及d随m的增大而减小时m的取值范围.
考点:二次函数综合题
专题:压轴题
分析:(1)根据直线解析式求出点A、B、C的坐标,然后利用待定系数法求出反比例函数解析式,再求出点D的坐标,再利用待定系数法求出二次函数解析式即可;
(2)根据抛物线和双曲线解析式求出点P、Q的坐标,然后根据平行于x轴的直线上两点间的距离的求法求解即可;
(3)分点M在AB、BC、CD上三种情况,根据直线、抛物线和双曲线的解析式表示出d,再根据二次函数的增减性解答.
(2)根据抛物线和双曲线解析式求出点P、Q的坐标,然后根据平行于x轴的直线上两点间的距离的求法求解即可;
(3)分点M在AB、BC、CD上三种情况,根据直线、抛物线和双曲线的解析式表示出d,再根据二次函数的增减性解答.
解答:解:(1)令y=0,则-x-1=0,
解得x=-1,
令x=0,则y=-1,
所以,点A(-1,0),B(0,-1),
x=3时,y=-3-1=-4,
所以,点C(3,-4),
设双曲线解析式为y=
(k≠0),
则
=-4,
解得k=-12,
所以,双曲线解析式为y=-
,
∵点D的纵坐标为-3,
∴-
=-3,
解得x=4,
∴点D(4,-3),
∵抛物线y=ax2+
x+c过点B、D,
∴
,
解得
,
∴抛物线的解析式为y=-
x2+
x-1;
(2)当y=-2时,-
x2+
x-1=-2,
整理得,x2-3x-2=0,
解得x1=
,x2=
,
∴点P的坐标为(
,-2)或(
,-2),
-
=-2,
解得x=6,
∴点Q的坐标为(6,-2),
∴PQ=6-
=
或PQ=6-
=
;
(3)①点M在AB上时,-1<m<0,
d=MN=(-m-1)-(-
m2+
m-1)=
m2-
m=
(m-
)2-
,
∴d随m的增大而减小,
②点M在BC上时,0<m<3,
d=MN=(-
m2+
m-1)-(-m-1)=-
m2+
m=-
(m-
)2+
,
∴m=
时,d有最大值为
,
<m<3时,d随m的增大而减小,
③点M在CD上时,3<m<4,
d=MN=(-
m2+
m-1)-(-
)=-
m2+
m+
-1,
由图可知,d随m的增大而减小,
综上所述,d的最大值是
,-1<m<0,
<m<3,3<m<4时,d随m的增大而减小.
解得x=-1,
令x=0,则y=-1,
所以,点A(-1,0),B(0,-1),
x=3时,y=-3-1=-4,
所以,点C(3,-4),
设双曲线解析式为y=
| k |
| x |
则
| k |
| 3 |
解得k=-12,
所以,双曲线解析式为y=-
| 12 |
| x |
∵点D的纵坐标为-3,
∴-
| 12 |
| x |
解得x=4,
∴点D(4,-3),
∵抛物线y=ax2+
| 3 |
| 2 |
∴
|
解得
|
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)当y=-2时,-
| 1 |
| 2 |
| 3 |
| 2 |
整理得,x2-3x-2=0,
解得x1=
3+
| ||
| 2 |
3-
| ||
| 2 |
∴点P的坐标为(
3+
| ||
| 2 |
3-
| ||
| 2 |
-
| 12 |
| x |
解得x=6,
∴点Q的坐标为(6,-2),
∴PQ=6-
3+
| ||
| 2 |
9-
| ||
| 2 |
3-
| ||
| 2 |
9+
| ||
| 2 |
(3)①点M在AB上时,-1<m<0,
d=MN=(-m-1)-(-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 8 |
∴d随m的增大而减小,
②点M在BC上时,0<m<3,
d=MN=(-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 8 |
∴m=
| 5 |
| 2 |
| 25 |
| 8 |
| 5 |
| 2 |
③点M在CD上时,3<m<4,
d=MN=(-
| 1 |
| 2 |
| 3 |
| 2 |
| 12 |
| m |
| 1 |
| 2 |
| 3 |
| 2 |
| 12 |
| m |
由图可知,d随m的增大而减小,
综上所述,d的最大值是
| 25 |
| 8 |
| 5 |
| 2 |
点评:本题是二次函数综合题型,主要利用了待定系数法求函数解析式(包括二次函数解析式,反比例函数解析式),二次函数与反比例函数图象上点的坐标特征,二次函数的增减性,综合题,但难点不大,(2)要注意点P有两个,(3)要注意分情况讨论.

练习册系列答案
相关题目
如果方程(a-b)x=|a-b|的解是x=-1,那么( )
| A、a=b | B、a>b |
| C、a≠b | D、a<b |
