题目内容
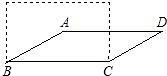如图，若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的正弦值为分析：作AE⊥BC于点E．根据面积的关系可以得到AB=2AE，根据正弦的定义即可求解．
解答：
解：作AE⊥BC于点E．
∵矩形的面积=BC•CF=2平行四边形ABCD的面积=2BC•AE
∴CF=2AE
∴sin∠ABC=
=
=
．
故答案是：
．
解：作AE⊥BC于点E．∵矩形的面积=BC•CF=2平行四边形ABCD的面积=2BC•AE
∴CF=2AE
∴sin∠ABC=
| AE |
| AB |
| AE |
| CF |
| 1 |
| 2 |
故答案是：
| 1 |
| 2 |
点评：本题主要考查了正弦函数的定义，根据面积的关系得到CF=2AE是解题的关键．
练习册系列答案
相关题目
13、如图，若将四根木条钉成的矩形木框变成平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的最小内角等于
