题目内容
已知AB是⊙O的弦，点P在AB上，且OP=2cm，PA=3cm，PB=4cm，则⊙O的半径为________cm．
4
分析：根据相交弦定理“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”进行计算．
解答：
解：作直线OP交⊙O于C、D两点，
∵⊙O的半径为4cm，OP=2cm，
∴PC=4-2=2cm，PD=4+2=6cm．
由相交弦定理得：PA•PB=PC•PD，
∴PB=
=
=4cm．
故答案为4．
点评：此题主要考查相交弦定理：圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等．
分析：根据相交弦定理“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”进行计算．
解答：
解：作直线OP交⊙O于C、D两点，∵⊙O的半径为4cm，OP=2cm，
∴PC=4-2=2cm，PD=4+2=6cm．
由相交弦定理得：PA•PB=PC•PD，
∴PB=
==4cm．故答案为4．
点评：此题主要考查相交弦定理：圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等．
练习册系列答案
阅读快车系列答案
相关题目
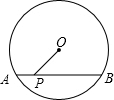已知AB是⊙O的弦，P是AB上一点，AB=10，PA=4，OP=5，求⊙O的半径．
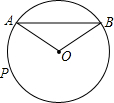如图，已知AB是⊙O的弦，半径OA=1cm，∠AOB=120°，⊙O上一动点P从A点出发，沿逆时针方向运动到B点，当S△POA=S△AOB时，则点P所经过的弧长（不考虑点P与点B重合的情形）是
如图，已知AB是⊙O的弦，半径OA=2cm，∠AOB=120°．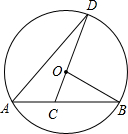
如图，已知AB是⊙O的弦，OB=1，∠B=30°，C是弦AB上一动点（不与A、B重合），连CO并延长交⊙O于点D，连AD．