题目内容
【附加题】阅读下面的材料,解答后面给出的问题:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式,例如
| a |
| a |
| 2 |
| 2 |
(1)请你再写出两个二次根式,使它们互为有理化因式:
这样,化简一个分母含有二次根式的式子时,采用分子、分母同乘以分母的有理化因式的方法就可以了,例如:
| ||
|
| ||||
|
| ||
| 3 |
| ||
3-
|
| ||||
(3-
|
3
| ||||
| 9-3 |
3
| ||||
| 6 |
(2)请仿照上面给出的方法化简下列各式:
①
3-2
| ||
3+2
|
| 1-b | ||
1-
|
(3)化简
| 3 | ||||
|
| 3 | ||||
|
3(
| ||||||||
(
|
| 5 |
| 2 |
| 3 | ||||
|
(
| ||||||||
|
| 5 |
| 2 |
A、甲的解法正确,乙的解法不正确B、甲的解法不正确,乙的解法正确
C、甲、乙的解法都正确D、甲、乙的解法都不正确
(4)已知a=
| 1 | ||
|
| 1 | ||
|
| a2+b2+7 |
A、5 B、6 C、3 D、4.
分析:(1)根据平方差公式,选择两个互为有理化的因式;
(2)可分子、分母同乘以分母的有理化因式,也可以将分子因式分解;
(3)这两种解法都正确,反映了分母有理化的两种方法;
(4)先将a、b分母有理化,再计算a2+b2的值,代入二次根式即可.
(2)可分子、分母同乘以分母的有理化因式,也可以将分子因式分解;
(3)这两种解法都正确,反映了分母有理化的两种方法;
(4)先将a、b分母有理化,再计算a2+b2的值,代入二次根式即可.
解答:解:(1)化为有理化因式的二次根式为
+
与
-
,答案不唯一;
(2)①
=
=17-12
;
②
=
=1+
;
(3)甲将分子、分母中同乘以分母的有理化因式,正确,
乙将分子分解因式,再约分,正确,
这两种方法都适合于二次根式的化简,故选C;
(4)∵a=
=
=
+2
b=
=
=
-2
∴a2+b2=(
+2)2+(
-2)2=18
则
=
=5.故选A.
| 5 |
| 2 |
| 5 |
| 2 |
(2)①
3-2
| ||
3+2
|
(3-2
| ||||
(3+2
|
| 2 |
②
| 1-b | ||
1-
|
(1+
| ||||
1-
|
| b |
(3)甲将分子、分母中同乘以分母的有理化因式,正确,
乙将分子分解因式,再约分,正确,
这两种方法都适合于二次根式的化简,故选C;
(4)∵a=
| 1 | ||
|
| ||||
(
|
| 5 |
b=
| 1 | ||
|
| ||||
(
|
| 5 |
∴a2+b2=(
| 5 |
| 5 |
则
| a2+b2+7 |
| 18+7 |
点评:本题考查了二次根式的分母有理化运算的方法,二次根式的运算问题.本题可先计算a2+b2,再代入二次根式中进行计算.

练习册系列答案
相关题目
 24、先阅读下面的材料,然后解答问题:
24、先阅读下面的材料,然后解答问题:
 的解为
的解为 ;
; 的解为
的解为 ;
; 的解为
的解为 ;
; 的解是________________;
的解是________________; 的解是___________________;
的解是___________________; 变形为方程
变形为方程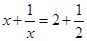 的解为
的解为 ;
; 的解为
的解为 ;
; 的解为
的解为 ;
; 的解是________________;
的解是________________; 的解是___________________;
的解是___________________; 变形为方程
变形为方程