题目内容
已知函数y=ax2+bx+z的图象如图所示，那么函数解析式为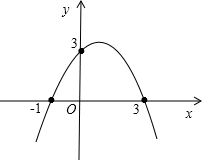
- A.y=-x2+2x+3
- B.y=x2-2x-3
- C.y=-x2-2x+3
- D.y=-x2-2x-3
A
分析：此题有两种解法：①直接用待定系数法求解；②用排除法：首先根据抛物线与y轴交点坐标，可判断出抛物线解析式的常数项为3，因此B、D可以被排除；然后将A点坐标代入A、C进行验证即可．
解答：由图知：抛物线经过点（-1，0），（3，0），（0，3）；
设抛物线的解析式为：y=a（x+1）（x-3），则有：
a（0+1）（0-3）=3，a=-1；
即：y=-（x+1）（x-3）=-x2+2x+3，
故选A．
点评：此题主要考查的是用待定系数法确定二次函数解析式的方法，应根据已知点坐标的特点灵活的选用合适的方法．
分析：此题有两种解法：①直接用待定系数法求解；②用排除法：首先根据抛物线与y轴交点坐标，可判断出抛物线解析式的常数项为3，因此B、D可以被排除；然后将A点坐标代入A、C进行验证即可．
解答：由图知：抛物线经过点（-1，0），（3，0），（0，3）；
设抛物线的解析式为：y=a（x+1）（x-3），则有：
a（0+1）（0-3）=3，a=-1；
即：y=-（x+1）（x-3）=-x2+2x+3，
故选A．
点评：此题主要考查的是用待定系数法确定二次函数解析式的方法，应根据已知点坐标的特点灵活的选用合适的方法．
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
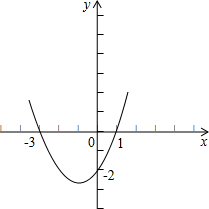已知函数y=ax2+bx+c的图象如图所示，试根据图象回答下列问题：