题目内容
设[x]表示最接近x的整数(x≠n+0、5,n为整数),则[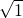 ]+[
]+[ ]+[
]+[ ]+…+[
]+…+[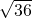 ]=
]=
- A.132
- B.146
- C.161
- D.666
B
分析:先计算出1.52,2.52,3.52,4.52,5.52,即可得出[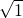 ],[
],[ ],[
],[ ]…[
]…[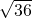 ]中有2个1,4个2,6个3,8个4,10个5,6个6,从而可得出答案.
]中有2个1,4个2,6个3,8个4,10个5,6个6,从而可得出答案.
解答:1.52=2.25,可得出有2个1;
2.52=6.25,可得出有4个2;
3.52=12.25,可得出有6个3;
4.52=20.25,可得出有8个4;
5.52=30.25,可得出有10个5;
则剩余6个数全为6.
故[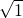 ]+[
]+[ ]+[
]+[ ]+…+[
]+…+[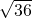 ]=1×2+2×4+3×6+4×8+5×10+6×6=146.
]=1×2+2×4+3×6+4×8+5×10+6×6=146.
故选B.
点评:本题考查了估算无理数的大小,难度较大,注意根据题意找出规律是关键.
分析:先计算出1.52,2.52,3.52,4.52,5.52,即可得出[
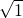 ],[
],[ ],[
],[ ]…[
]…[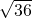 ]中有2个1,4个2,6个3,8个4,10个5,6个6,从而可得出答案.
]中有2个1,4个2,6个3,8个4,10个5,6个6,从而可得出答案.解答:1.52=2.25,可得出有2个1;
2.52=6.25,可得出有4个2;
3.52=12.25,可得出有6个3;
4.52=20.25,可得出有8个4;
5.52=30.25,可得出有10个5;
则剩余6个数全为6.
故[
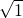 ]+[
]+[ ]+[
]+[ ]+…+[
]+…+[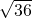 ]=1×2+2×4+3×6+4×8+5×10+6×6=146.
]=1×2+2×4+3×6+4×8+5×10+6×6=146.故选B.
点评:本题考查了估算无理数的大小,难度较大,注意根据题意找出规律是关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
设[x]表示最接近x的整数(x≠n+0.5,n为整数),则[
]+[
]+[
]+…+[
]=( )
| 1 |
| 2 |
| 3 |
| 36 |
| A、132 | B、146 |
| C、161 | D、666 |
设[x]表示最接近x的整数(x≠n+0.5,n为整数),则[
]+[
]+[
]+…+[
]的值为( )
| 1×2 |
| 2×3 |
| 3×4 |
| 100×101 |
| A、5151 | B、5150 |
| C、5050 | D、5049 |