题目内容
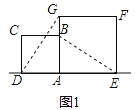
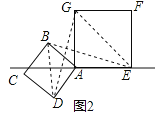
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线l上,AB与AG在同一直线上.
(1)图1中,小明发现DG=BE,请你帮他说明理由.
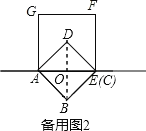
(2)小明将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,请你直接写出此时BE的长.
【答案】(1)见解析;(2)BE的长为![]() 或
或![]() .
.
【解析】分析:(1)根据正方形的性质得出AD=AB,AG=AE,![]() 再利用SAS证明△DAG≌△BAE, 根据全等三角形对应边相等即可得出DG=BE;
再利用SAS证明△DAG≌△BAE, 根据全等三角形对应边相等即可得出DG=BE;
(2)分两种情况:①C在EA的延长线上时,连结BD交AC于O,求出OB、OE,然后在Rt△BOE中,利用勾股定理可求出BE的长;②C在AE上时,证明C与E重合,那么![]()
详解:(1)如图1,∵四边形ABCD与四边形AEFG都是正方形,
∴AD=AB,AG=AE,![]()
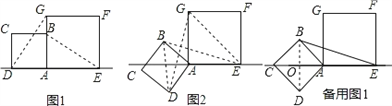
在△DAG与△BAE中,
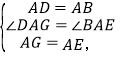
∴△DAG≌△BAE,
∴DG=BE;
(2)将正方形ABCD按如图2那样绕点A旋转一周,旋转到当点C恰好落在直线l上时,分两种情况:
①如果C在EA的延长线上时,
如备用图1,连结BD交AC于O,
∵正方形ABCD边长为![]() ,
,
∴![]()
∴OB=OA=12BD=1.
∵正方形AEFG边长为2,
∴OE=OA+AE=1+2=3.
在Rt△BOE中,∵![]()
∴![]()
②如果C在AE上时,
如备用图2,连结BD交AC于O,
∵正方形ABCD边长为![]() ,
,
∴![]()
∵正方形AEFG边长为2,
∴AE=2,
∴C与E重合,
∴![]()
故所求BE的长为![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
第一次 | 第二次 | 第三次 | 第四次 | |
甲 | 87 | 95 | 85 | 93 |
乙 | 80 | 80 | 90 | 90 |
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为S甲2=17、S乙2=25,下列说法正确的是( )
A. 甲同学四次数学测试成绩的平均数是89分
B. 甲同学四次数学测试成绩的中位数是90分
C. 乙同学四次数学测试成绩的众数是80分
D. 乙同学四次数学测试成绩较稳定