题目内容
【题目】眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a﹣b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.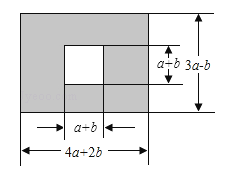
【答案】解:由题意得:
绿化的面积为:(4a+2b)(3a﹣b)﹣(a+b)2=12a2﹣4ab+6ab﹣2b2﹣(a2+2ab+b2)
=12a2+2ab﹣2b2﹣a2﹣2ab﹣b2
=11a2﹣3b2 ,
当a=20,b=10时,
原式=11×202﹣3×102=4400﹣300=4100.
【解析】根据长方形面积公式表示出长方形的面积,再根据正方形面积公式表示出正方形的面积,两个面积相减即可得出绿化的面积,再把a,b的值代入即可得出绿化面积.
【考点精析】通过灵活运用多项式乘多项式和完全平方公式,掌握多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加;首平方又末平方,二倍首末在中央.和的平方加再加,先减后加差平方即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目